Pregunta 24

Un joven universitario quiso modelar la relación entre sus horas de estudio diarias, y sus horas de sueño. Para esto, cada día que estudió en cierto mes, registró su tiempo de estudio $x_i$ (en horas), para luego anotar el tiempo que empleó para dormir aquella misma noche $y_i$ (en horas). Finalizado el mes, obtuvo un total de $n=24$ mediciones $\left(x_i, y_i\right)$ que se resumen con los siguientes estadísticos.

$$\begin{gathered} \bar{x}=3,80, \quad \bar{y}=5,74, \quad \sum_{i=1}^n\left(x_i-\bar{x}\right)^2=57,4, \\ \sum_{i=1}^n\left(y_i-\bar{y}\right)^2=38,11, \quad \sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)=-27,7 \end{gathered}$$

El joven ajustó una recta de regresión simple a estos datos, y al visualizar el ajuste, notó que había cierta tendencia lineal, pero que aún existían variaciones alrededor de la recta. Un promedio de estas variaciones no explicadas por el modelo se estima a través del error cuadrático medio (o MSE en inglés).

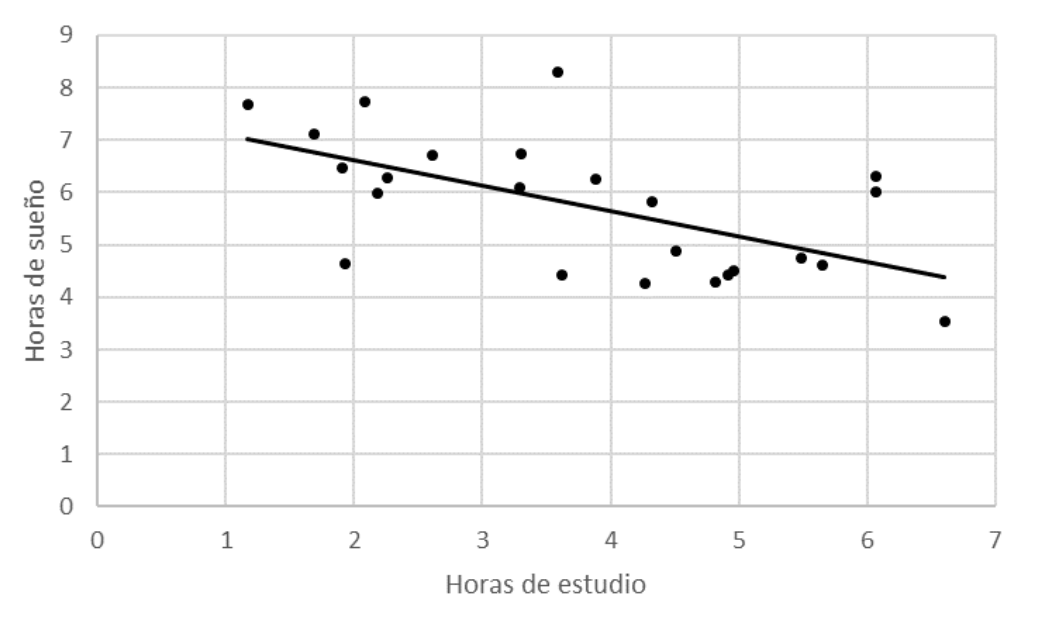
En base a esta muestra, ¿cuál de las siguientes alternativas corresponde al valor más cercano al error cuadrático medio del modelo?

a) 1,12

b) 1,69

c) 10,02

d) 24,74

Solución propuesta

Aún no hay solución propuesta 🥲

info

Si este ejercicio tiene una solución, podría estar incorrecta. Si deseas proponer una solución alternativa, manda tu solución abriendo un Pull Request en el repositorio de GitHub con el archivo .mdx correspondiente.

Comentarios