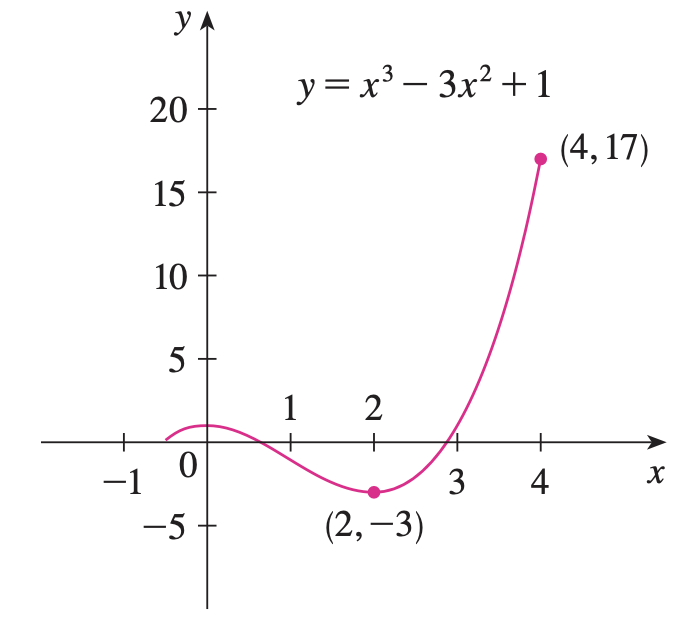Cálculo I
Gráficos de funciones
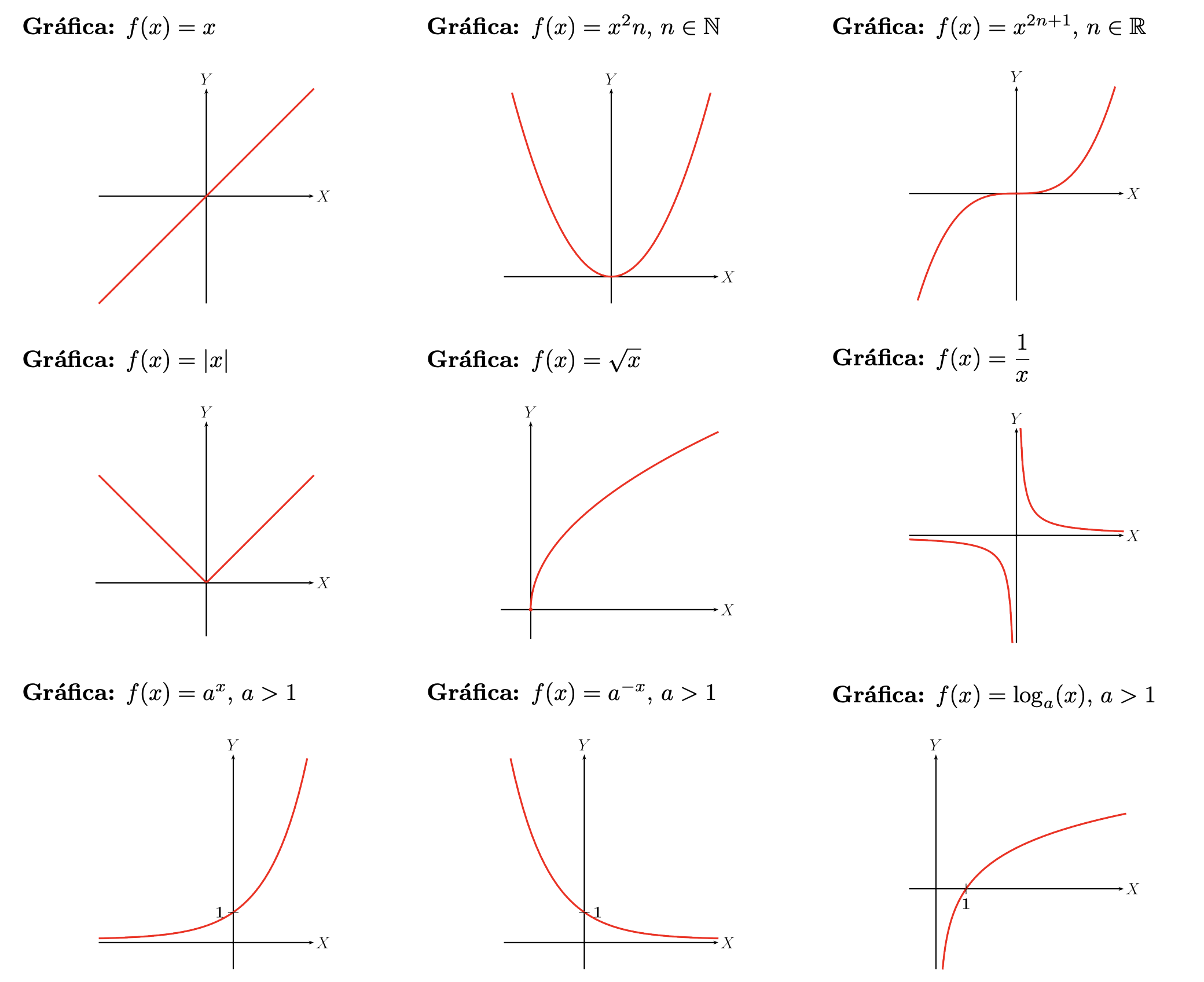
Los gráficos de funciones básicas, exponenciales y logarítmicas son:
Derivadas
La derivada de una función f f f x = a x = a x = a f ′ ( a ) f'(a) f ′ ( a )
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h f^{\prime}(a) = \lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h} f ′ ( a ) = h → 0 lim h f ( a + h ) − f ( a ) si este límite existe.
A continuación se presentan las derivadas de las funciones más comunes:
Función Derivada Derivada con regla de la cadena Potencia d d x [ x n ] = n x n − 1 \frac{d}{d x}\left[x^n\right]=n x^{n-1} d x d [ x n ] = n x n − 1 d d x [ u n ] = n u n − 1 ⋅ u ′ \frac{d}{d x}\left[u^n\right]=n u^{n-1} \cdot u^{\prime} d x d [ u n ] = n u n − 1 ��⋅ u ′ Exponencial (base e e e d d x [ e x ] = e x \frac{d}{d x}\left[e^x\right]=e^x d x d [ e x ] = e x d d x [ e u ] = e u ⋅ u ′ \frac{d}{d x}\left[e^u\right]=e^u \cdot u^{\prime} d x d [ e u ] = e u ⋅ u ′ Exponencial (base a a a d d x [ a x ] = a x ln ( a ) \frac{d}{d x}\left[a^x\right]=a^x \ln (a) d x d [ a x ] = a x ln ( a ) d d x [ a u ] = a u ln ( a ) ⋅ u ′ \frac{d}{d x}\left[a^u\right]=a^u \ln (a) \cdot u^{\prime} d x d [ a u ] = a u ln ( a ) ⋅ u ′ Logaritmo Natural d d x [ ln ( x ) ] = 1 x \frac{d}{d x}[\ln (x)]=\frac{1}{x} d x d [ ln ( x )] = x 1 d d x [ ln ( u ) ] = 1 u ⋅ u ′ \frac{d}{d x}[\ln (u)]=\frac{1}{u} \cdot u^{\prime} d x d [ ln ( u )] = u 1 ⋅ u ′ u ′ u \frac{u^{\prime}}{u} u u ′ Logaritmo (base a a a d d x [ log a ( x ) ] = 1 x ⋅ ln ( a ) \frac{d}{d x}\left[\log _a(x)\right]=\frac{1}{x \cdot \ln (a)} d x d [ log a ( x ) ] = x ⋅ l n ( a ) 1 d d x [ log a ( u ) ] = 1 u ⋅ ln ( a ) ⋅ u ′ \frac{d}{d x}\left[\log _a(u)\right]=\frac{1}{u \cdot \ln (a)} \cdot u^{\prime} d x d [ log a ( u ) ] = u ⋅ l n ( a ) 1 ⋅ u ′ Seno d d x [ sin ( x ) ] = cos ( x ) \frac{d}{d x}[\sin (x)]=\cos (x) d x d [ sin ( x )] = cos ( x ) d d x [ sin u ] = cos ( u ) ⋅ u ′ \frac{d}{d x}[\sin u]=\cos (u) \cdot u^{\prime} d x d [ sin u ] = cos ( u ) ⋅ u ′ Coseno d d x [ cos ( x ) ] = − sin ( x ) \frac{d}{d x}[\cos (x)]=-\sin (x) d x d [ cos ( x )] = − sin ( x ) d d x [ cos u ] = �− sin ( u ) ⋅ u ′ \frac{d}{d x}[\cos u]=-\sin (u) \cdot u^{\prime} d x d [ cos u ] = − sin ( u ) ⋅ u ′ Tangente d d x [ tan ( x ) ] = sec 2 ( x ) \frac{d}{d x}[\tan (x)]=\sec ^2(x) d x d [ tan ( x )] = sec 2 ( x ) d d x [ tan ( u ) ] = sec 2 ( u ) ⋅ u ′ \frac{d}{d x}[\tan (u)]=\sec ^2(u) \cdot u^{\prime} d x d [ tan ( u )] = sec 2 ( u ) ⋅ u ′ Cosecante d d x [ csc ( x ) ] = − csc ( x ) cot ( x ) \frac{d}{d x}[\csc (x)]=-\csc (x) \cot (x) d x d [ csc ( x )] = − csc ( x ) cot ( x ) d d x [ csc ( u ) ] = − csc ( u ) cot ( u ) ⋅ u ′ \frac{d}{d x}[\csc (u)]=-\csc (u) \cot (u) \cdot u^{\prime} d x d [ csc ( u )] = − csc ( u ) cot ( u ) ⋅ u ′ Secante d d x [ sec ( x ) ] = sec ( x ) tan ( x ) \frac{d}{d x}[\sec (x)]=\sec (x) \tan (x) d x d [ sec ( x )] = sec ( x ) tan ( x ) d d x [ sec ( u ) ] = sec ( u ) tan ( u ) ⋅ u ′ \frac{d}{d x}[\sec (u)]=\sec (u) \tan (u) \cdot u^{\prime} d x d [ sec ( u )] = sec ( u ) tan ( u ) ⋅ u ′ Cotangente d d x [ cot ( x ) ] = − csc 2 ( x ) \frac{d}{d x}[\cot (x)]=-\csc ^2(x) d x d [ cot ( x )] = − csc 2 ( x ) d d x [ cot ( u ) ] = − csc 2 ( u ) ⋅ u ′ \frac{d}{d x}[\cot (u)]=-\csc ^2(u) \cdot u^{\prime} d x d [ cot ( u )] = − csc 2 ( u ) ⋅ u ′ Arcoseno d d x sin − 1 ( x ) = 1 1 − x 2 \frac{d}{d x} \sin ^{-1}(x)=\frac{1}{\sqrt{1-x^2}} d x d sin − 1 ( x ) = 1 − x 2 1 d d x sin − 1 ( u ) = 1 1 − u 2 ⋅ u ′ \frac{d}{d x} \sin ^{-1}(u)=\frac{1}{\sqrt{1-u^2}} \cdot u^{\prime} d x d sin − 1 ( u ) = 1 − u 2 1 ⋅ u ′ Arcocoseno d d x cos − 1 ( x ) = − 1 1 − x 2 \frac{d}{d x} \cos ^{-1}(x)=\frac{-1}{\sqrt{1-x^2}} d x d cos − 1 ( x ) = 1 − x 2 − 1 d d x cos − 1 ( u ) = − 1 1 − u 2 ⋅ u ′ \frac{d}{d x} \cos ^{-1}(u)=\frac{-1}{\sqrt{1-u^2}} \cdot u^{\prime} d x d cos − 1 ( u ) = 1 − u 2 − 1 ⋅ u ′ Arcotangente d d x tan − 1 ( x ) = 1 1 + x 2 \frac{d}{d x} \tan ^{-1}(x)=\frac{1}{1+x^2} d x d tan − 1 ( x ) = 1 + x 2 1 d d x tan − 1 ( u ) = 1 1 + u 2 ⋅ u ′ \frac{d}{d x} \tan ^{-1}(u)=\frac{1}{1+u^2} \cdot u^{\prime} d x d tan − 1 ( u ) = 1 + u 2 1 ⋅ u ′ Arcocosecante d d x csc − 1 ( x ) = − 1 ∥ x ∥ x 2 − 1 \frac{d}{d x} \csc ^{-1}(x)=\frac{-1}{\|x\| \sqrt{x^2-1}} d x d csc − 1 ( x ) = ∥ x ∥ x 2 − 1 − 1 d d x csc − 1 ( u ) = − 1 ∥ u ∥ u 2 − 1 ⋅ u ′ \frac{d}{d x} \csc ^{-1}(u)=\frac{-1}{\|u\| \sqrt{u^2-1}} \cdot u^{\prime} d x d csc − 1 ( u ) = ∥ u ∥ u 2 − 1 − 1 ⋅ u ′ Arcosecante d d x sec − 1 ( x ) = 1 ∥ x ∥ x 2 − 1 \frac{d}{d x} \sec ^{-1}(x)=\frac{1}{\|x\| \sqrt{x^2-1}} d x d sec − 1 ( x ) = ∥ x ∥ x 2 − 1 1 d d x sec − 1 ( u ) = 1 ∥ u ∥ u 2 − 1 ⋅ u ′ \frac{d}{d x} \sec ^{-1}(u)=\frac{1}{\|u\| \sqrt{u^2-1}} \cdot u^{\prime} d x d sec − 1 ( u ) = ∥ u ∥ u 2 − 1 1 ⋅ u ′ Arcocotangente d d x cot − 1 ( x ) = − 1 1 + x 2 \frac{d}{d x} \cot ^{-1}(x)=\frac{-1}{1+x^2} d x d cot − 1 ( x ) = 1 + x 2 − 1 d d x cot − 1 ( u ) = − 1 1 + u 2 ⋅ u ′ \frac{d}{d x} \cot ^{-1}(u)=\frac{-1}{1+u^2} \cdot u^{\prime} d x d cot − 1 ( u ) = 1 + u 2 − 1 ⋅ u ′
Propiedades analíticas de los gráficos
Máximos y mínimos
Sea c c c D D D f f f f ( c ) f(c) f ( c )
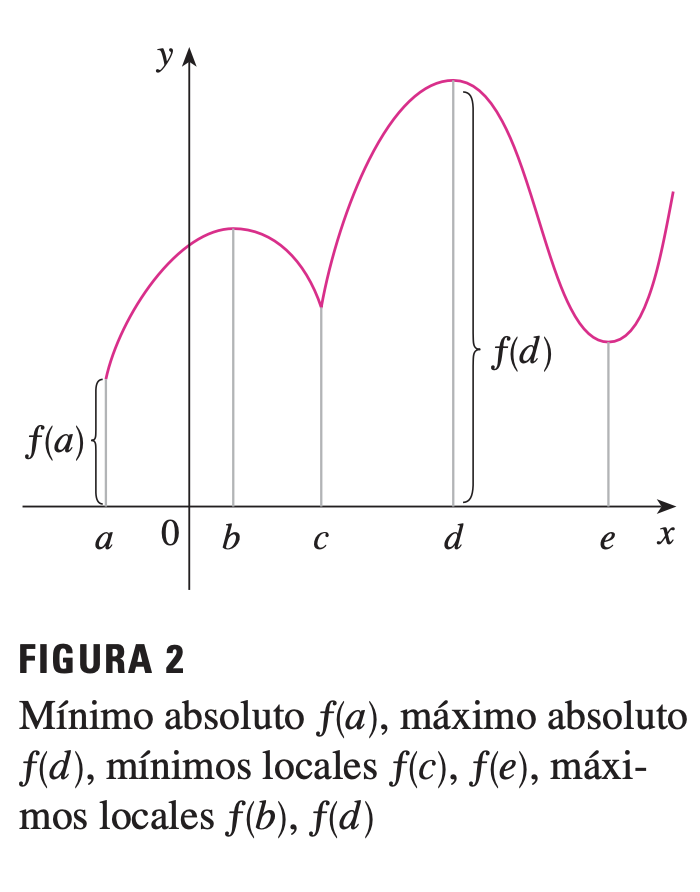
valor máximo absoluto de f f f D D D f ( c ) ⩾ f ( x ) f(c) \geqslant f(x) f ( c ) ⩾ f ( x ) x x x D D D
valor mínimo absoluto de f f f D D D f ( c ) ⩽ f ( x ) f(c) \leqslant f(x) f ( c ) ⩽ f ( x ) x x x D D D
El número f ( c ) f(c) f ( c )
valor máximo local de f f f f ( c ) ⩾ f ( x ) f(c) \geqslant f(x) f ( c ) ⩾ f ( x ) x x x c c c
valor mínimo local de f f f f ( c ) ⩽ f ( x ) f(c) \leqslant f(x) f ( c ) ⩽ f ( x ) x x x c c c
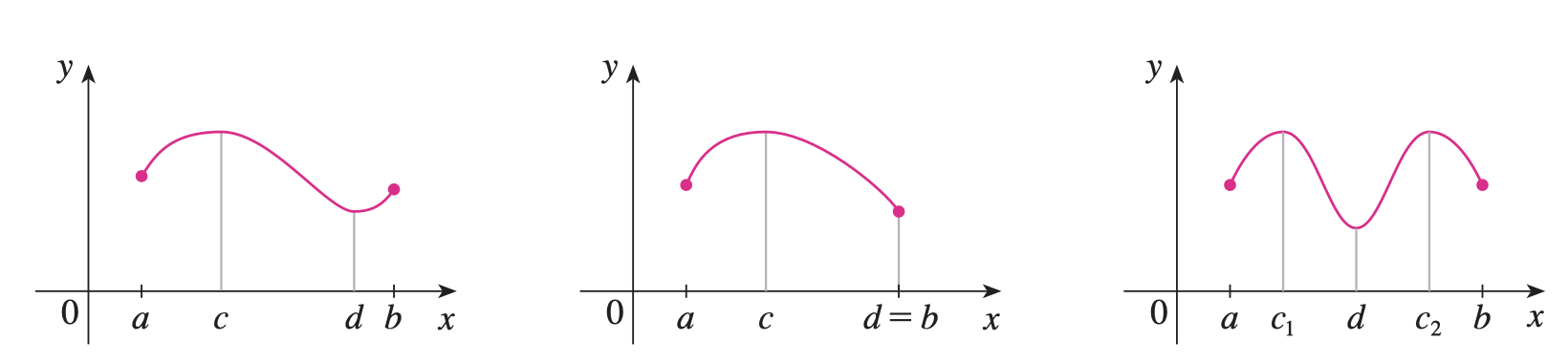
Teorema del valor extremo
Si f f f [ a , b ] [a, b] [ a , b ] f f f f ( c ) f(c) f ( c ) f ( d ) f(d) f ( d ) c c c d d d [ a , b ] [a, b] [ a , b ]
Teorema del valor extremo Teorema de Fermat
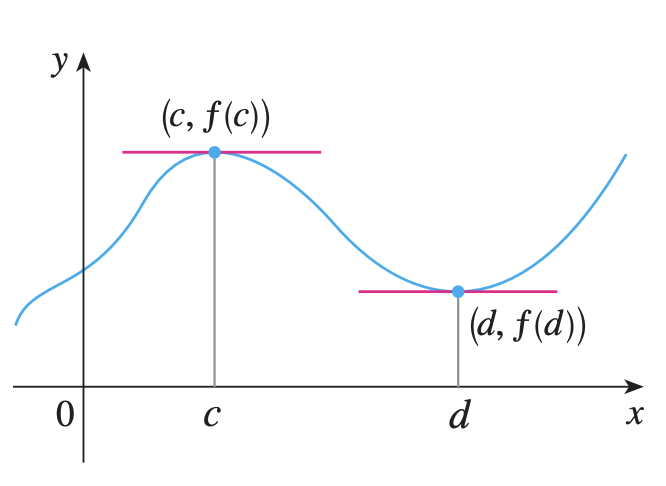
Si f f f c c c f ′ ( c ) f'(c) f ′ ( c ) f ′ ( c ) = 0 f'(c) = 0 f ′ ( c ) = 0
Teorema de Fermat Números críticos
Un número crítico de una función f f f c c c f f f f ′ ( c ) = 0 f'(c) = 0 f ′ ( c ) = 0 f ′ ( c ) f'(c) f ′ ( c )
Método del intervalo cerrado
Para hallar los valores máximo y mínimo absolutos de una función continua f f f [ a , b ] [a, b] [ a , b ]
Encuentre los valores de f f f f f f ( a , b ) (a, b) ( a , b )
Halle los valores de f f f
El más grande de los valores de los pasos 1 y 2 es el valor máximo absoluto; el más pequeño, el valor mínimo absoluto.
Ejemplo de método del intervalo cerrado Teorema del valor medio
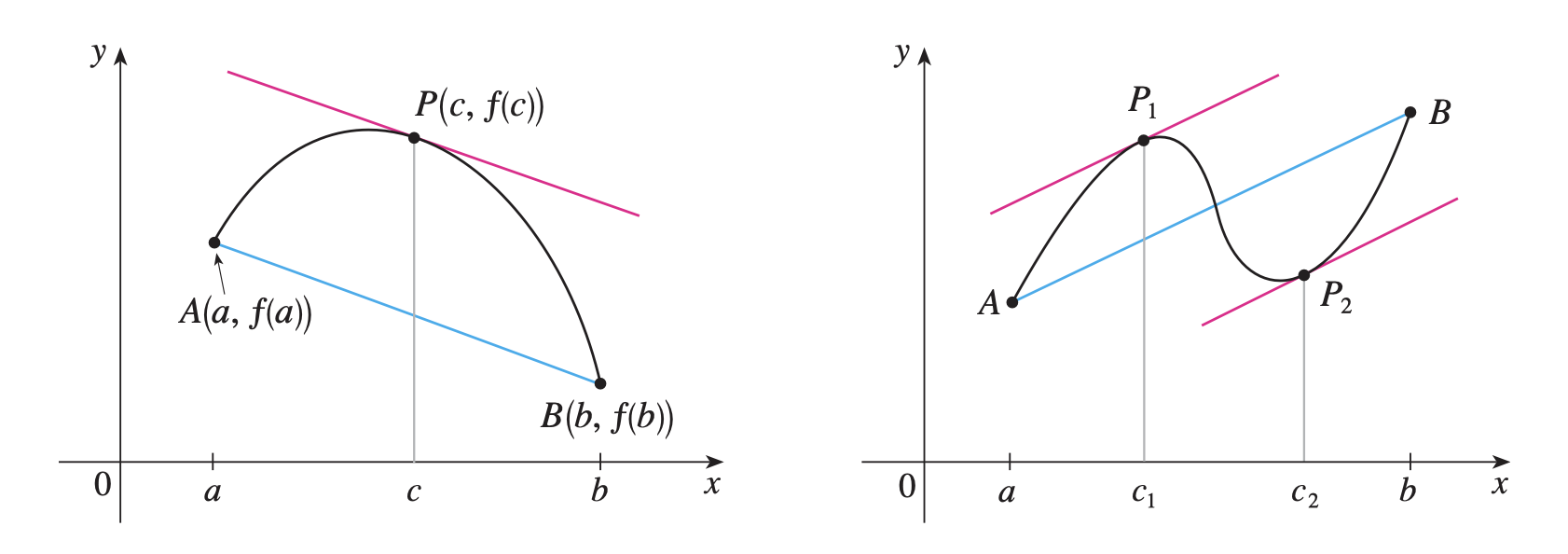
Si f f f
f f f [ a , b ] [a, b] [ a , b ] f f f ( a , b ) (a, b) ( a , b ) x = c x=c x = c ( a , b ) (a, b) ( a , b )
f ′ ( c ) = f ( b ) − f ( a ) b − a f^{\prime}(c)=\frac{f(b)-f(a)}{b-a} f ′ ( c ) = b − a f ( b ) − f ( a ) o, equivalentemente,
f ( b ) − f ( a ) = f ′ ( c ) ( b − a ) f(b)-f(a)=f^{\prime}(c)(b-a) f ( b ) − f ( a ) = f ′ ( c ) ( b − a ) Teorema del valor medio Prueba de crecimiento y decrecimiento
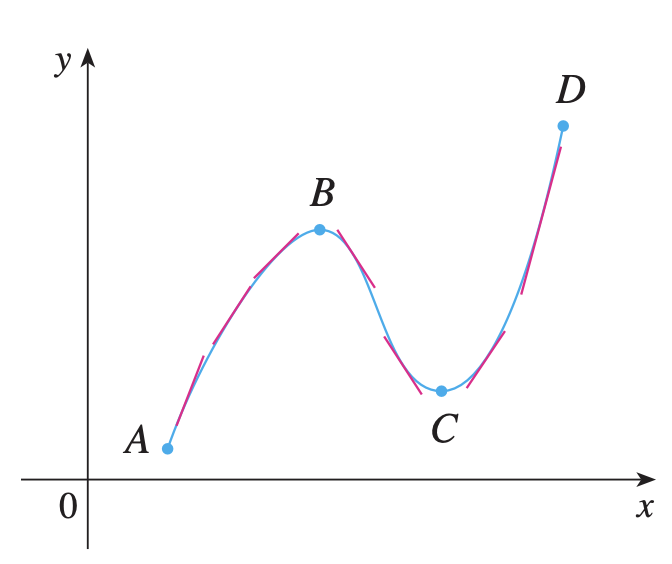
Si f ′ ( x ) > 0 f'(x) > 0 f ′ ( x ) > 0 x x x f f f
Si f ′ ( x ) < 0 f'(x) < 0 f ′ ( x ) < 0 x x x f f f
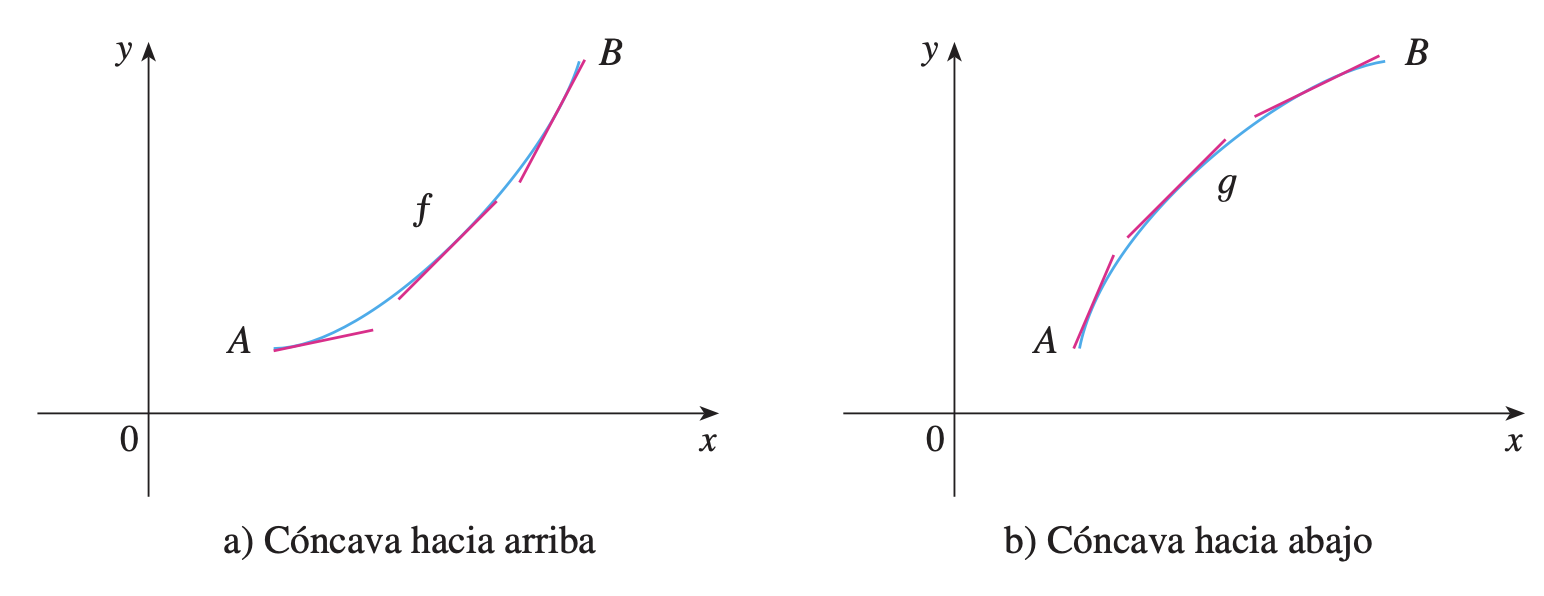
Prueba creciente/decreciente Prueba de concavidad
Si f ′ ′ ( x ) > 0 f''(x) > 0 f ′′ ( x ) > 0 x x x f f f
Si f ′ ′ ( x ) < 0 f''(x) < 0 f ′′ ( x ) < 0 x x x f f f
Asíntotas
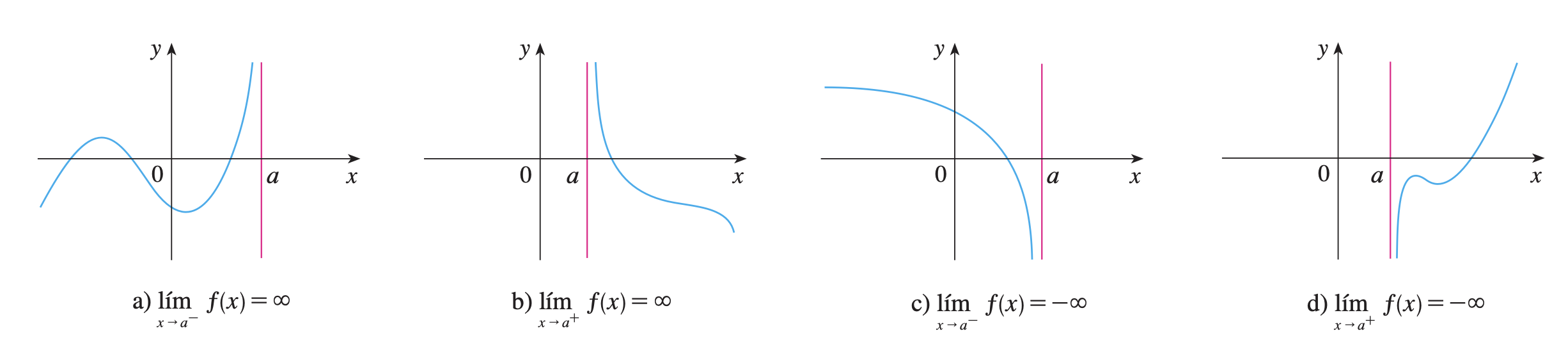
La recta x = a x=a x = a asíntota vertical de la curva y = f ( x ) y=f(x) y = f ( x )
lim x → a f ( x ) = ∞ lim x → a − f ( x ) = ∞ lim x → a + f ( x ) = ∞ lim x → a f ( x ) = − ∞ lim x → a − f ( x ) = − ∞ lim x → a + f ( x ) = − ∞ \begin{array}{lll}
\displaystyle{\lim _{x \rightarrow a} f(x)=\infty} & \displaystyle{\lim _{x \rightarrow a^{-}} f(x)=\infty} & \displaystyle{\lim _{x \rightarrow a^{+}} f(x)=\infty} \\[20pt]
\displaystyle{\lim _{x \rightarrow a} f(x)=-\infty} & \displaystyle{\lim _{x \rightarrow a^{-}} f(x)=-\infty} & \displaystyle{\lim _{x \rightarrow a^{+}} f(x)=-\infty}
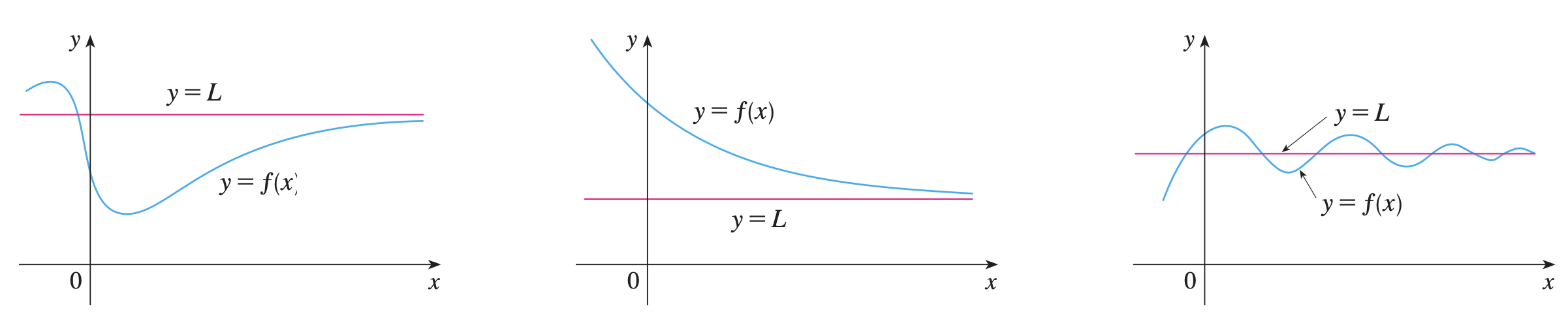
\end{array} x → a lim f ( x ) = ∞ x → a lim f ( x ) = − ∞ x → a − lim f ( x ) = ∞ x → a − lim f ( x ) = − �∞ x → a + lim f ( x ) = ∞ x → a + lim f ( x ) = − ∞ Asíntotas verticales La recta y = L y=L y = L asíntota horizontal de la curva y = f ( x ) y=f(x) y = f ( x )
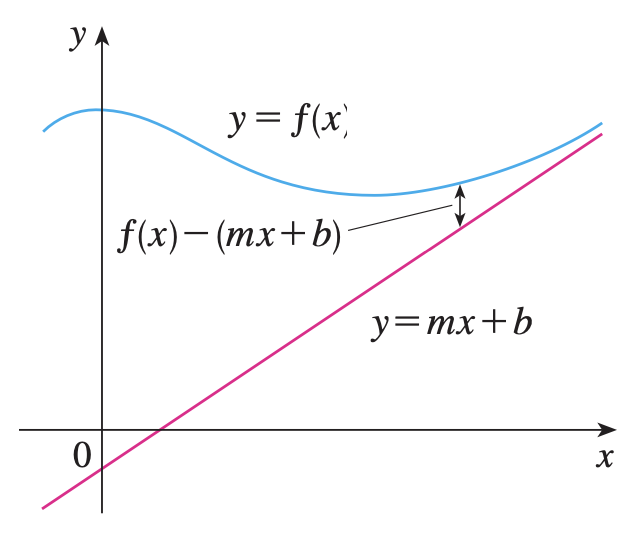
lim x → ∞ f ( x ) = L o lim x → − ∞ f ( x ) = L \lim _{x \rightarrow \infty} f(x)=L \quad \text { o } \quad \lim _{x \rightarrow-\infty} f(x)=L x → ∞ lim f ( x ) = L o x → − ∞ lim f ( x ) = L Asíntotas horizontales Algunas curvas tienen asíntotas que son oblicuas ; esto es, no son horizontales ni verticales. Si
lim x → ∞ [ f ( x ) − ( m x + b ) ] = 0 \lim _{x \rightarrow \infty}[f(x)-(m x+b)]=0 x → ∞ lim [ f ( x ) − ( m x + b )] = 0 entonces la recta y = m x + b y=m x+b y = m x + b
Asíntotas oblicuas