Cálculo III
Integrales múltiples
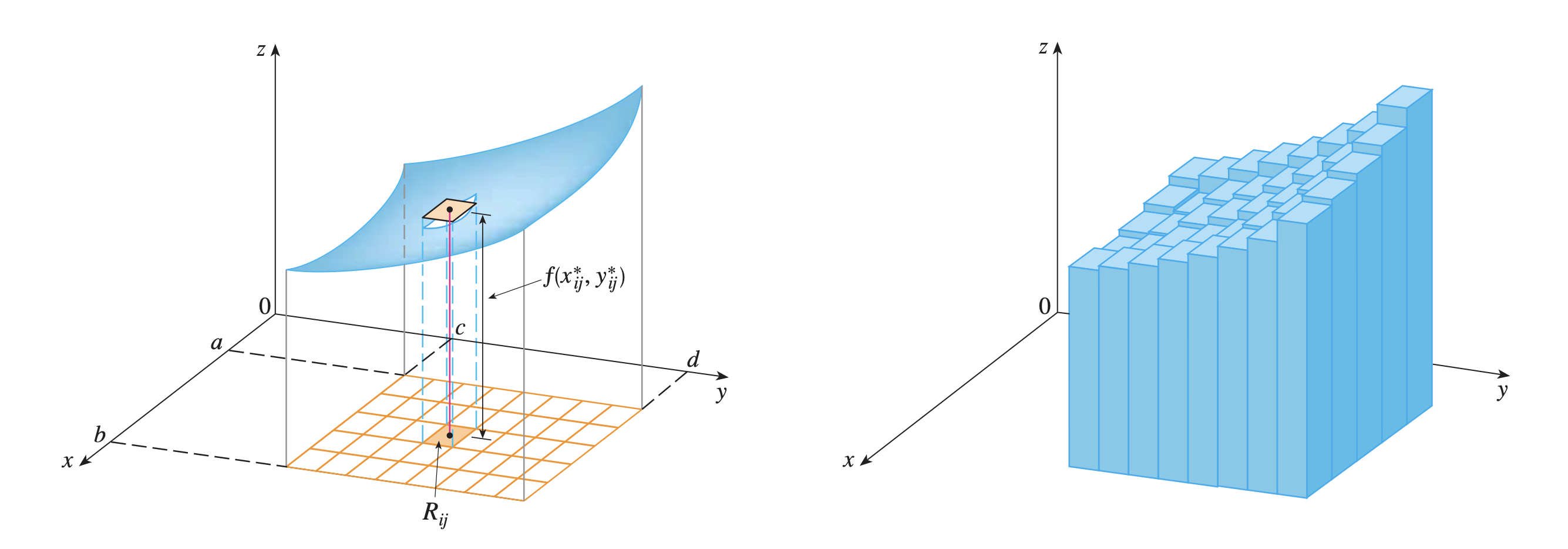
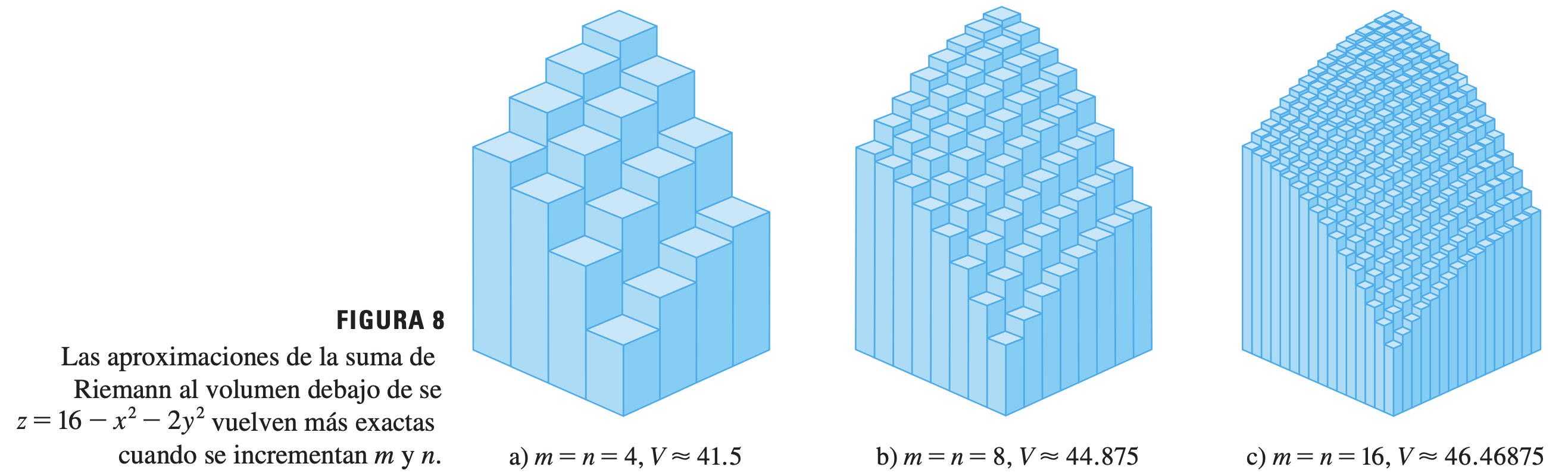
La integral doble de f f f R R R
∬ R f ( x , y ) d A = lim m , n → ∞ ∑ i = 1 m ∑ j = 1 n f ( x i , y j ) Δ A \iint_R f(x, y) d A=\lim _{m, n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f\left(x_i, y_j\right) \Delta A ∬ R f ( x , y ) d A = m , n → ∞ lim i = 1 ∑ m j = 1 ∑ n f ( x i , y j ) Δ A si el límite existe.
Integral doble Volumen
Si f ( x , y ) ⩾ 0 f(x, y) \geqslant 0 f ( x , y ) ⩾ 0 V V V R R R z = f ( x , y ) z=f(x, y) z = f ( x , y )
V = ∬ R f ( x , y ) d A V=\iint_R f(x, y) d A V = ∬ R f ( x , y ) d A Momentos y centros de masa
Los momentos de una lámina plana que ocupa una región D D D δ ( x , y ) \delta(x, y) δ ( x , y )
M x = ∬ D y δ ( x , y ) d A M y = ∬ D x δ ( x , y ) d A M_x=\iint_D y \,\delta(x, y) d A \qquad\qquad M_y=\iint_D x \,\delta(x, y) d A M x = ∬ D y δ ( x , y ) d A M y = ∬ D x δ ( x , y ) d A donde M x M_x M x x x x M y M_y M y y y y
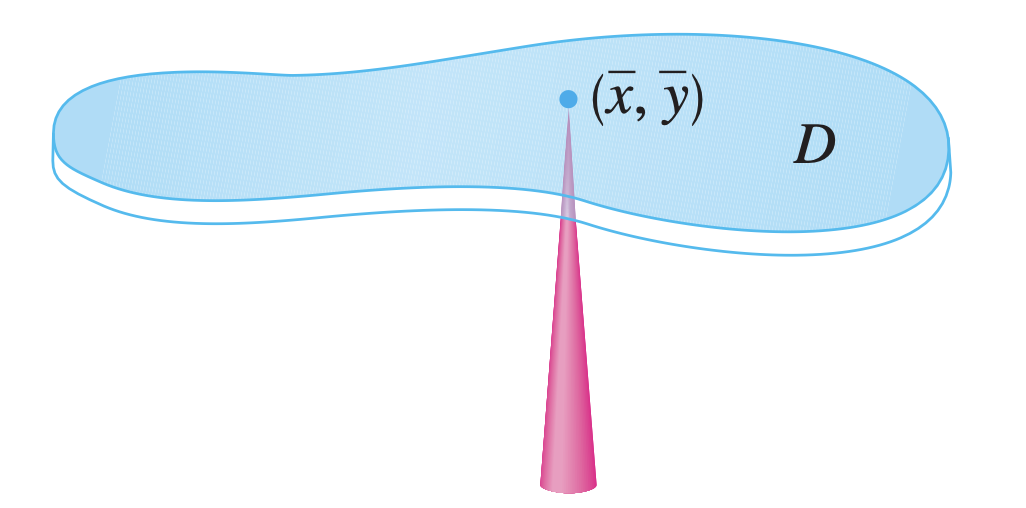
Con los momentos, podemos encontrar el centro de masa ( x ˉ , y ˉ ) (\bar{x}, \bar{y}) ( x ˉ , y ˉ )
x ˉ = M y m = 1 m ∬ D x ρ ( x , y ) d A y ˉ = M x m = 1 m ∬ D y ρ ( x , y ) d A \bar{x}=\frac{M_y}{m}=\frac{1}{m} \iint_D x \rho(x, y) d A \qquad\qquad \bar{y}=\frac{M_x}{m}=\frac{1}{m} \iint_D y \rho(x, y) d A x ˉ = m M y = m 1 ∬ D x ρ ( x , y ) d A y ˉ = m M x = m 1 ∬ D y ρ ( x , y ) d A donde la masa m m m
m = ∬ D ρ ( x , y ) d A m=\iint_D \rho(x, y) d A m = ∬ D ρ ( x , y ) d A Centro de masa Curvas de nivel
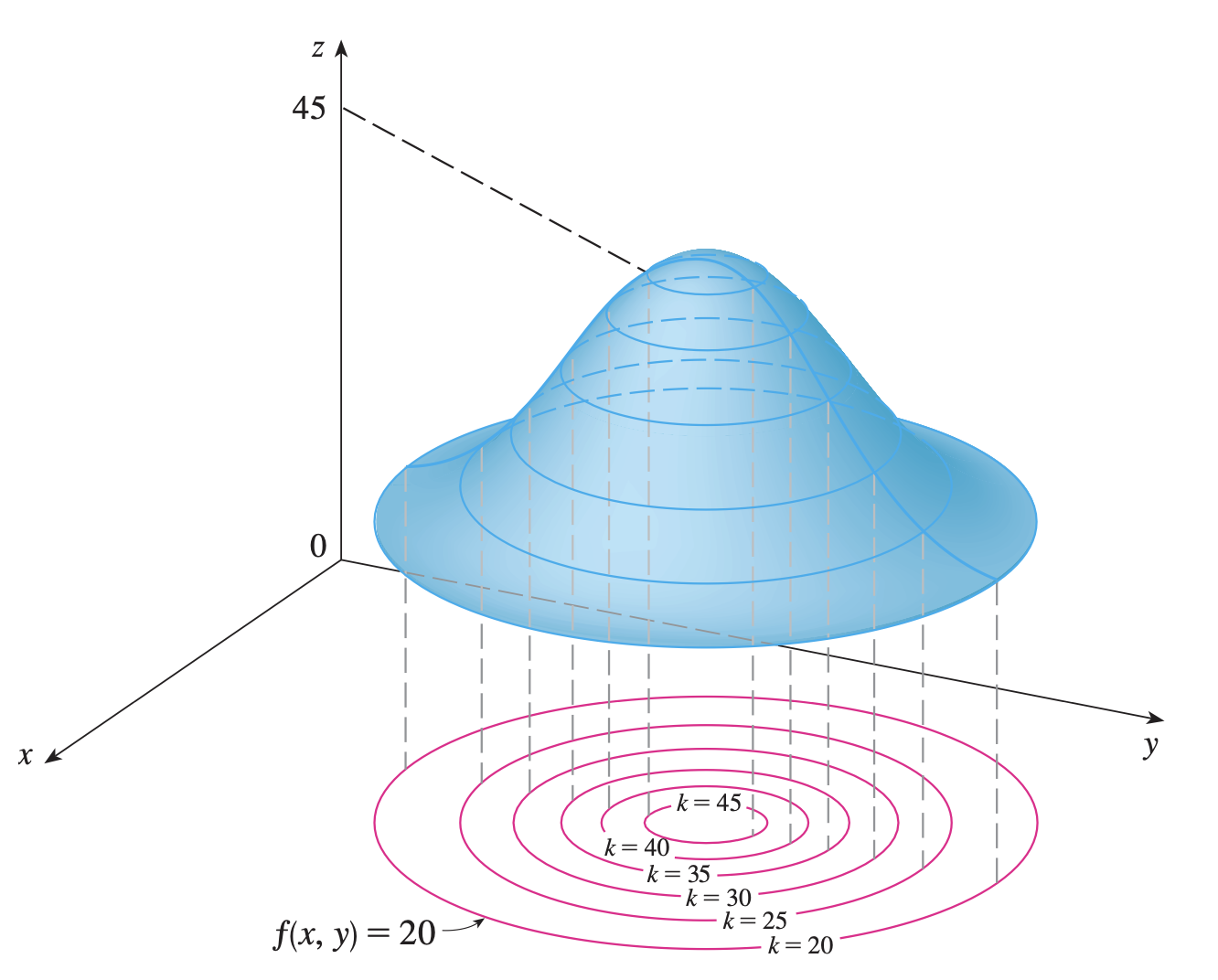
Las curvas de nivel de una función f f f f ( x , y ) = k f(x, y)=k f ( x , y ) = k k k k f f f
Curvas de nivel Derivadas direccionales
Definición
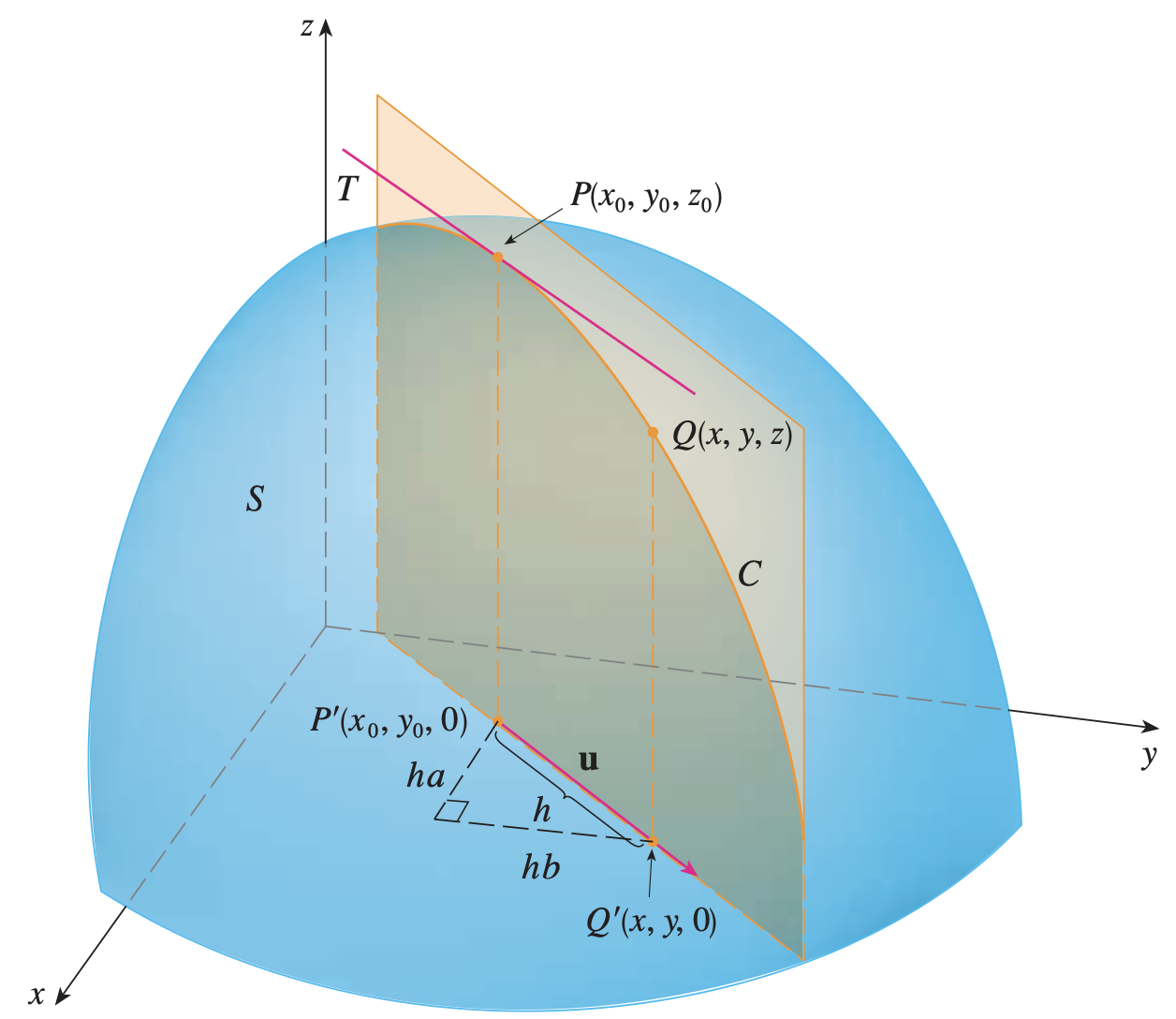
La derivada direccional de f f f ( x 0 , y 0 ) \left(x_0, y_0\right) ( x 0 , y 0 ) u = ⟨ a , b ⟩ \mathbf{u}=\langle a, b\rangle u = ⟨ a , b ⟩
D u f ( x 0 , y 0 ) = lim h → 0 f ( x 0 + h a , y 0 + h b ) − f ( x 0 , y 0 ) h D_{\mathbf{u}} f\left(x_0, y_0\right)=\lim _{h \rightarrow 0} \frac{f\left(x_0+h a, y_0+h b\right)-f\left(x_0, y_0\right)}{h} D u f ( x 0 , y 0 ) = h → 0 lim h f ( x 0 + ha , y 0 + hb ) − f ( x 0 , y 0 ) si este límite existe.
Derivada direccional Si f f f x x x y y y f f f derivada direccional en la dirección de cualquier vector unitario u = ⟨ a , b ⟩ \mathbf{u}=\langle a, b\rangle u = ⟨ a , b ⟩
D u f ( x , y ) = f x ( x , y ) a + f y ( x , y ) b D_{\mathrm{u}} f(x, y)=f_x(x, y) a+f_y(x, y) b D u f ( x , y ) = f x ( x , y ) a + f y ( x , y ) b Gradiente
Si f f f x x x y y y gradiente de f f f ∇ f \nabla f ∇ f
∇ f ( x , y ) = ⟨ f x ( x , y ) , f y ( x , y ) ⟩ = ∂ f ∂ x i + ∂ f ∂ y j \nabla f(x, y)=\left\langle f_x(x, y), f_y(x, y)\right\rangle=\frac{\partial f}{\partial x} \mathbf{i}+\frac{\partial f}{\partial y} \mathbf{j} ∇ f ( x , y ) = ⟨ f x ( x , y ) , f y ( x , y ) ⟩ = ∂ x ∂ f i + ∂ y ∂ f j Con esta notación para el vector gradiente, podemos escribir la expresión para la derivada direccional como
D u f ( x , y ) = ∇ f ( x , y ) ⋅ u D_{\mathbf{u}} f(x, y)=\nabla f(x, y) \cdot \mathbf{u} D u f ( x , y ) = ∇ f ( x , y ) ⋅ u Máximo de la derivada direccional
Supongamos que f f f valor máximo de la derivada direccional D u f ( x ) D_{\mathbf{u}} f(\mathbf{x}) D u f ( x ) ∣ ∇ f ( x ) ∣ |\nabla f(\mathbf{x})| ∣∇ f ( x ) ∣ u \mathbf{u} u ∇ f ( x ) \nabla f(\mathbf{x}) ∇ f ( x )