Cálculo II

Integral definida

El área $A$ de la región $S$ que se encuentra bajo la gráfica de la función continua $f$ es el límite de la suma de las áreas de los rectángulos de aproximación:

$$A=\lim _{n \rightarrow \infty} R_n=\lim _{n \rightarrow \infty}\left[f\left(x_1\right) \Delta x+f\left(x_2\right) \Delta x+\cdots+f\left(x_n\right) \Delta x\right]$$

Suma de Riemman

Si $f$ es una función continua definida para $a \leqslant x \leqslant b$, dividimos el intervalo $[a, b]$ en $n$ subintervalos de igual ancho $\Delta x=(b-a) / n$. Sean $x_0(=a), x_1, x_2, \ldots, x_n(=b)$ los puntos extremos de estos subintervalos y sean $x_1^*, x_2^*, \ldots, x_n^*$ los puntos muestra en estos subintervalos, de modo que $x_i^*$ se encuentre en el $i$-ésimo subintervalo $\left[x_{i-1}, x_i\right]$. Entonces la integral definida de $f$, desde $a$ hasta $b$, es

$$\int_a^b f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^n f\left(x_i^*\right) \Delta x$$

siempre que este límite exista y dé el mismo valor para todos las posibles elecciones de los puntos muestra. Si existe, decimos que $f$ es integrable sobre $[a, b]$.

Integral definida

Propiedades de la integral definida

Cuando se definió la integral definida $\int_a^b f(x) d x$, de manera implícita se supuso que $a<b$. Pero la definición como un límite de la suma de Riemann tiene sentido aun cuando $a>b$. Note que si invertimos $a$ y $b$, entonces $\Delta x$ cambia de $(b-a) / n$ a $(a-b) / n$. En consecuencia,

$$\int_b^a f(x) d x=-\int_a^b f(x) d x$$

Si $a=b$, entonces $\Delta x=0$ de manera que

$$\int_a^a f(x) d x=0$$

Otras propiedades:

1. $\displaystyle\int_a^b c d x=c(b-a)$, donde $c$ es cualquier constante
2. $\displaystyle\int_a^b[f(x)+g(x)] d x=\int_a^b f(x) d x+\int_a^b g(x) d x$
3. $\displaystyle\int_a^b c f(x) d x=c \int_a^b f(x) d x$, donde $c$ es cualquier constante
4. $\displaystyle\int_a^b[f(x)-g(x)] d x=\int_a^b f(x) d x-\int_a^b g(x) d x$
5. $\displaystyle\int_a^c f(x) d x+\int_c^b f(x) d x=\int_a^b f(x) d x$

Teorema fundamental del cálculo

Suponga que $f$ es continua sobre $[a, b]$.

1. Si $\displaystyle g(x)=\int_a^x f(t) d t$, entonces $g^{\prime}(x)=f(x)$.
2. $\displaystyle \int_a^b f(x) d x=F(b)-F(a)$, donde $F$ es cualquier antiderivada de $f$; es decir, $F^{\prime}=f$.

Criterios de convergencia

Para series, la siguiente tabla resume los criterios de convergencia:

Criterio	Cuando usar	Conclusión
Serie geométrica	$\displaystyle \sum_{n=0}^{\infty} a r^n$	Converge si $\lvert r \rvert<1$, diverge si $\lvert r \rvert \geq 1$
Test de la divergencia	Cualquier serie $\displaystyle \sum_{n=1}^{\infty} a_n$	Si $\displaystyle \lim_{n \to \infty} a_n \neq 0$, entonces la serie diverge
Serie $p$	$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^p}$	Converge si $p>1$, diverge si $p \leq 1$
Test de comparación	$\displaystyle \sum_{n=1}^{\infty} a_n$ y $\displaystyle \sum_{n=1}^{\infty} b_n$, con $0 \leq a_n \leq b_n$	Si $\displaystyle \sum_{n=1}^{\infty} b_n$ converge, entonces $\displaystyle \sum_{n=1}^{\infty} a_n$ converge Si $\displaystyle \sum_{n=1}^{\infty} a_n$ diverge, entonces $\displaystyle \sum_{n=1}^{\infty} b_n$ diverge
Test de comparación en el límite	$\displaystyle \sum_{n=1}^{\infty} a_n$ y $\displaystyle \sum_{n=1}^{\infty} b_n$, con $a_n, b_n > 0$	Si $\displaystyle \lim_{n \to \infty} \frac{a_n}{b_n}=c$, donde $c$ es una constante positiva, entonces $\displaystyle \sum_{n=1}^{\infty} a_n$ y $\displaystyle \sum_{n=1}^{\infty} b_n$ convergen o divergen juntas
Serie alternante	$\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1} a_n$ o $\displaystyle \sum_{n=1}^{\infty} (-1)^n a_n$, con $a_n > 0$	Converge si $\displaystyle \lim_{n \to \infty} a_n=0$ y $a_n \geq a_{n+1}$ para todo $n$
Convergencia absoluta	Series $\displaystyle \sum_{n=1}^{\infty} a_n$ con valores positivos y negativos	Si $\displaystyle \sum_{n=1}^{\infty} \lvert a_n \rvert$ converge, entonces $\displaystyle \sum_{n=1}^{\infty} a_n$ converge
Test de la integral	$\displaystyle \sum_{n=1}^{\infty} f(n)$	Si $\displaystyle f(x)$ es una función decreciente y positiva para $x \geq 1$, entonces $\displaystyle \sum_{n=1}^{\infty} f(n)$ converge si y solo si $\displaystyle \int_{1}^{\infty} f(x) d x$ converge
Test de la razón	Series $\displaystyle \sum_{n=1}^{\infty} a_n$ que especialmente son exponenciales o factoriales	Si $\displaystyle \lim_{n \to \infty} \left\lvert \frac{a_{n+1}}{a_n} \right\rvert=L$, entonces $\displaystyle \sum_{n=1}^{\infty} a_n$ converge si $L<1$ y diverge si $L>1$. Si $L = 1$, el test es inconcluso
Test de la raíz	Series $\displaystyle \sum_{n=1}^{\infty} a_n$ qie especialmente son exponenciales	Si $\displaystyle \lim_{n \to \infty} \sqrt[n]{\lvert a_n \rvert}=L$, entonces $\displaystyle \sum_{n=1}^{\infty} a_n$ converge si $L<1$ y diverge si $L>1$. Si $L = 1$, el test es inconcluso

Ecuaciones de rectas y planos en el espacio

Rectas

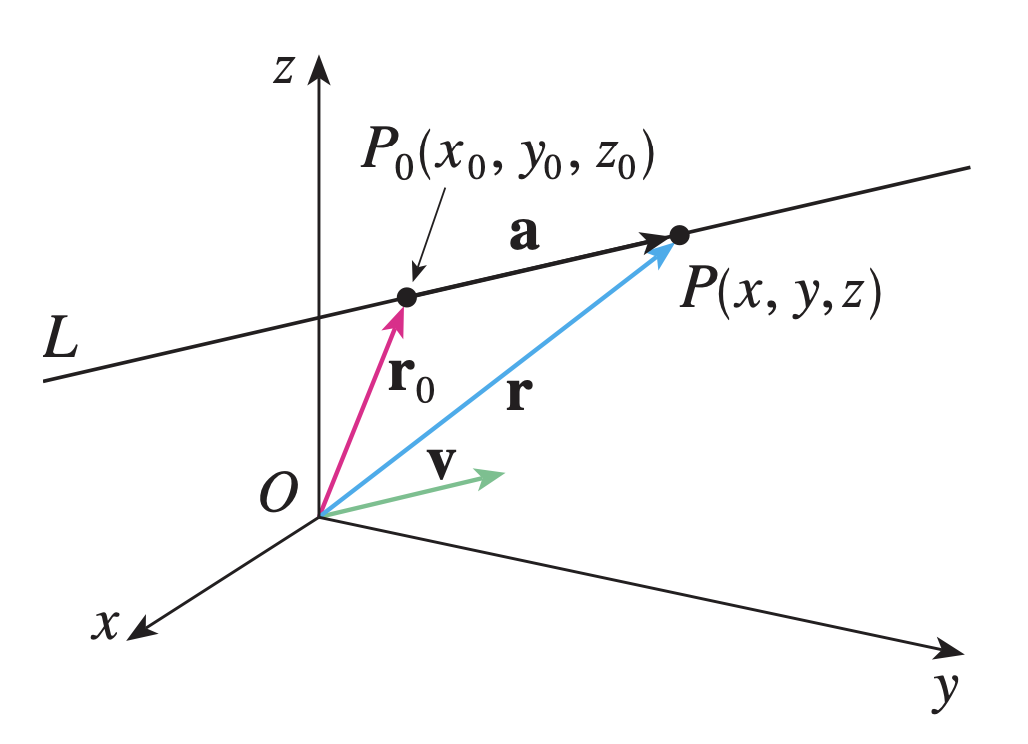
La ecuación vectorial de la recta está dada por

$$\vec{r} = \vec{r}_0 + t \vec{v}$$

donde $\vec{r}_0$ es un punto de la recta y $\vec{v}$ es un vector paralelo a la recta.

La ecuación paramétrica de la recta está dada por

$$\begin{cases} x = x_0 + at \\ y = y_0 + bt \\ z = z_0 + ct \end{cases}$$

mientras que la ecuación simétrica de la recta está dada por

$$\frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c}$$

donde $(x_0, y_0, z_0)$ es un punto de la recta y $(a, b, c)$ es un vector paralelo a la recta.

Recta en el espacio

Planos

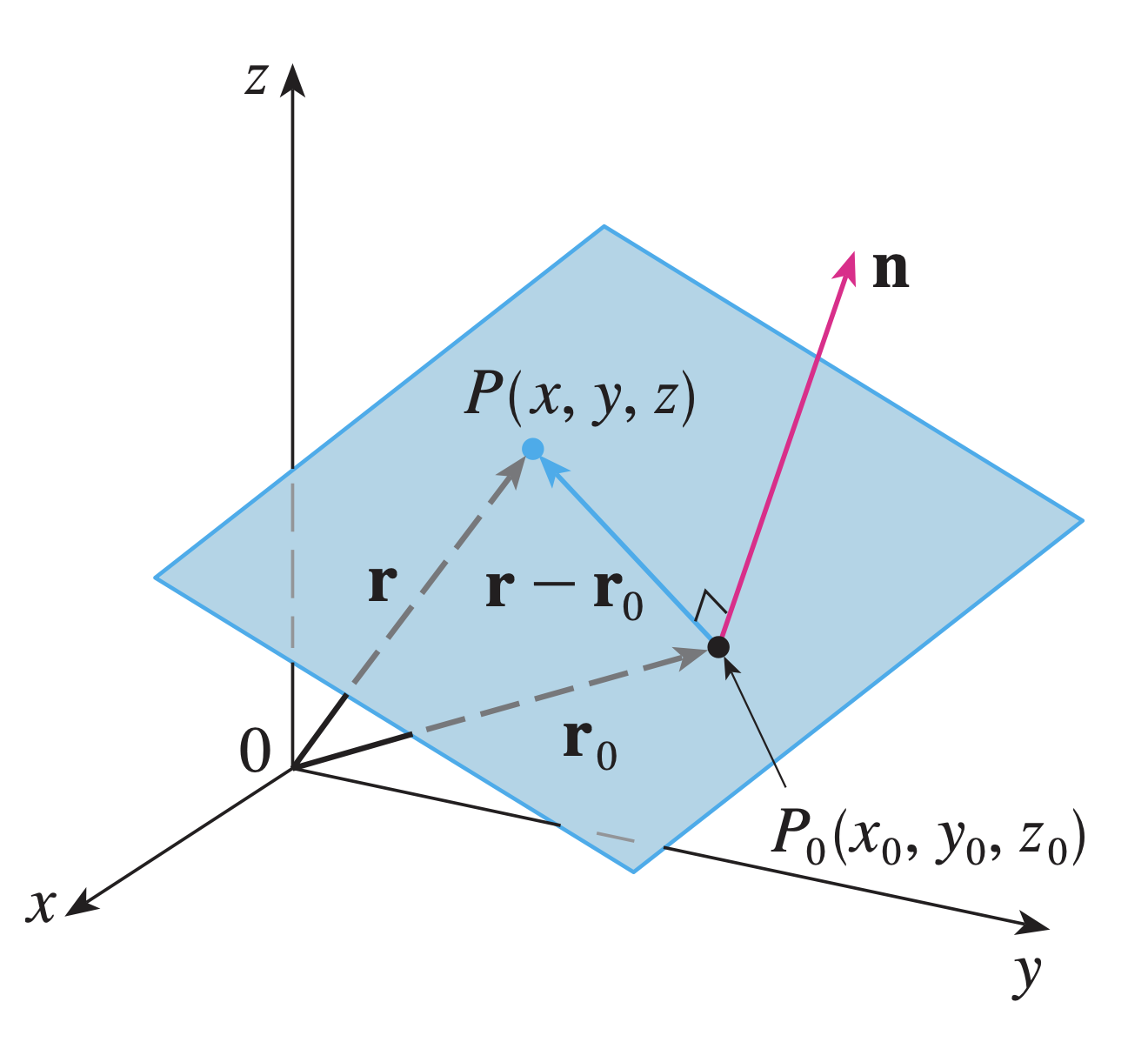
La ecuación vectorial de un plano está dada por

$$\vec{n} \cdot (\vec{r} - \vec{r}_0) = 0$$

donde $\vec{r}_0$ es un punto del plano y $\vec{n}$ es un vector normal al plano.

La ecuación escalar de un plano está dada por

$$a(x-x_0) + b(y-y_0) + c(z-z_0) = 0$$

donde $(x_0, y_0, z_0)$ es un punto del plano y $(a, b, c)$ es un vector normal al plano.

Si se reescriben los términos de la ecuación anterior, podemos establecer la ecuación lineal del plano como

$$ax + by + cz = d$$

donde $d = ax_0 + by_0 + cz_0$.

Plano en el espacio