Inferencia estadística

Definiciones y propiedades

En los capítulos previos hemos visto de manera introductoria como, dada una distribución $\left(p_X(x), f_X(x) \circ F_X(x)\right)$ de una variable aleatoria $X$ y el valor de sus parámetros, obtener probabilidades.

El calculo de probabilidades depende del valor de los parámetros. Por tanto, nos interesa disponer de métodos que permitan seleccionar adecuadamente valores de estos para las distribuciones de importancia práctica.

Para realizar lo anteriormente expuesto, requerimos información "del mundo real". Por ejemplo, datos referente a la pluviosidad en cierta área, intensidad y frecuencia de los movimientos telúricos, conteos, velocidades y flujo de vehículos en cierta intersección o vía, etc.

Con base a estos datos, los parámetros pueden ser estimados estadísticamente, y con información sobre el fenómeno inferir la distribución de probabilidad.

$$\begin{array}{c} \text{Mundo real} \\ \downarrow \\ \text{Colección de datos} \\ \downarrow \\ \text{Estimación de parámetros (escoger distribución)} \\ \downarrow \\ \text{Calculo de probabilidades} \\ \downarrow \\ \text{Información para Decidir - Hacer - Diseñar} \end{array}$$

La estimación clásica de parámetros consiste en dos tipos:

• Puntual: simplemente indica un valor único, basado en los datos, para representar el parámetro de interés.
• Intervalar: entrega un conjunto de valores (intervalo) donde el parámetro puede estar con cierto nivel de confianza.

Para un estimador puntual, las siguientes propiedades son deseables:

• Insesgamiento: valor esperado del estimador sea igual al parámetro de interés.
• Consistencia: implica que si $n \rightarrow \infty$, el estimador converge al parámetro (propiedad asintótica).
• Eficiencia: se refiere a que la varianza del estimador. Dado un conjunto de datos, $\theta_1$ es más eficiente que $\theta_2$ para estimar $\theta$ si tiene menor varianza.
• Suficiencia: un estimador se dice suficiente si utiliza toda la información contenida en la muestra para estimar el parámetro.

Métodos de estimación

Método de los Momentos

En términos generales, el método propone igualar los momentos teóricos no centrales de una variable aleatoria $X$ denotados por $\mu_k$, con los momentos empíricos, basados en los datos, $m_k$, y despejar los parámetros de interés. Es decir,

$$\begin{gathered} \mu_k=E\left(X^k\right) \quad \text { y } \quad m_k=\frac{1}{n} \sum_{i=1}^n x_i^k \\ \Rightarrow \mu_k=m_k, \quad k=1,2, \ldots \end{gathered}$$

Método de Máxima Verosimilitud

Otro método de estimación puntual es el denominado método de máxima verosimilitud (MV). En contraste con el método de los momentos, el método de máxima verosimilitud deriva directamente en estimador puntual del parámetro de interés.

Sea $X$ variable aleatoria con función de probabilidad $f_X(x, \theta)$, donde $\theta$ es el parámetro de interés. Dada una muestra (es decir, valores observados) $x_1, \ldots, x_n$, nos preguntamos cuál es el valor más probable de $\theta$ que produzca estos valores. En otras palabras, para los diferentes valores de $\theta$, cuál es el valor que maximiza la verosimilitud de los valores observados $x_1, \ldots, x_n$.

La función de verosimilitud de una muestra aleatoria $x_1, \ldots, x_n$, es decir, independiente e idénticamente distribuida es:

$$\begin{aligned} L\left(x_1, x_2, \ldots, x_n, \theta\right) & =f_{X_1, \ldots, X_n}\left(x_1, \ldots, x_n, \theta\right) \\ & =f_{X_1}\left(x_1, \theta\right) \times \cdots \times f_{X_n}\left(x_n, \theta\right), \quad \text { por independencia } \\ & =\prod_{i=1}^n f_X\left(x_i, \theta\right), \quad \text { por idéntica distribución } \end{aligned}$$

Se define el estimador de máxima verosimilitud (EMV) como el valor de $\theta$ que maximiza la función de verosimilitud $L$. Es decir, es la solución de

$$\frac{\partial}{\partial \theta} L\left(x_1, x_2, \ldots, x_n, \theta\right)=0 \Rightarrow \hat{\theta}=\theta$$

Maximizar $L$ es equivalente a maximizar $\ln L$, es decir,

$$\frac{\partial}{\partial \theta} \ln L\left(x_1, x_2, \ldots, x_n, \theta\right)=0$$

Si la función de distribución (discreta o continua) depende de más de un parámetro, digamos $\theta_1, \ldots, \theta_m$, los EMV respectivos son las soluciones de las $m$ ecuaciones:

$$\frac{\partial}{\partial \theta_j} \ln L\left(x_1, x_2, \ldots, x_n, \theta_1, \ldots, \theta_m\right)=0 \quad j=1,2, \ldots, m$$

Nota

Los EMV son estimadores que poseen las propiedades deseables descritas anteriormente. En particular, para $n$ grande, son "los mejores" estimadores (en el sentido de varianza mínima).

Propiedades

• Asintóticamente Insesgados: $E(\hat{\theta}_n) \rightarrow \theta$, cuando $n \rightarrow \infty$.
• Varianza alcanza la cota de Cramer-Rao:

$$\operatorname{Var}(\hat{\theta}_n)=\frac{1}{I_n(\theta)},$$

con $I_n(\theta)=-E\left[\dfrac{\partial^2}{\partial \theta^2} \ln(L(\theta))\right]$.

• Distribución Asintótica: Normal.
• Invarianza: Si $\hat{\theta}_n$ es el estimador máximo verosímil de $\theta$, entonces $g(\hat{\theta}_n)$ es el estimador máximo verosímil de $g(\theta)$ cuya distribución asintótica es

$$g(\hat{\theta})\, \dot{\sim} \,\text {Normal}\left(g(\theta), \sqrt{\frac{\left[g^{\prime}(\theta)\right]^2}{I_n(\theta)}}\right)$$

Prueba de Hipótesis

Una prueba de hipótesis es un método estadístico inferencial para la toma de decisiones sobre una población en base a la información proporcionada por los datos de una muestra. La inferencia puede hacerse con respecto a uno o más parámetros de la población o también para un modelo de distribución.

Una hipótesis es una afirmación con respecto a uno o más parámetros de una población.

Usualmente son dos las hipótesis que se contrastan son:

• Hipótesis nula, $\mathrm{H}_0$. Este tipo de hipótesis es la que se somete a prueba.
• Hipótesis alternativa, $\mathrm{H}_a$. Este tipo de hipótesis es la que se acepta si se rechaza la hipótesis nula.

Cuando interesa inferir sobre el valor de un parámetro $\mu$ de la población las hipótesis a contrastar son generalmente:

$$\mathrm{H}_0: \mu=\mu_0 \quad \text { vs } \quad \mathrm{H}_a: \mu \neq \mu_0$$

Procedimiento

Los pasos necesarios en las pruebas de hipótesis son:

1. Defina la hipótesis nula y alternativa.

$$\begin{array}{lll} \mathrm{H}_0: \mu=\mu_0 & \text { vs } & \mathrm{H}_a: \mu \neq \mu_0 \\ \mathrm{H}_0: \mu=\mu_0 & \text { vs } \quad & \mathrm{H}_a: \mu>\mu_0 \\ \mathrm{H}_0: \mu=\mu_0 & \text { vs } & \mathrm{H}_a: \mu<\mu_0 \end{array}$$

2. Identificar la prueba estadística adecuada y su distribución.
3. Basado en una muestra de datos observados estime el estadístico de prueba.
4. Especifique el nivel de significancia.

Dado que el estadístico de prueba es una variable aleatoria, la probabilidad de una decisión errónea puede ser controlada. Los errores que se pueden cometer son:

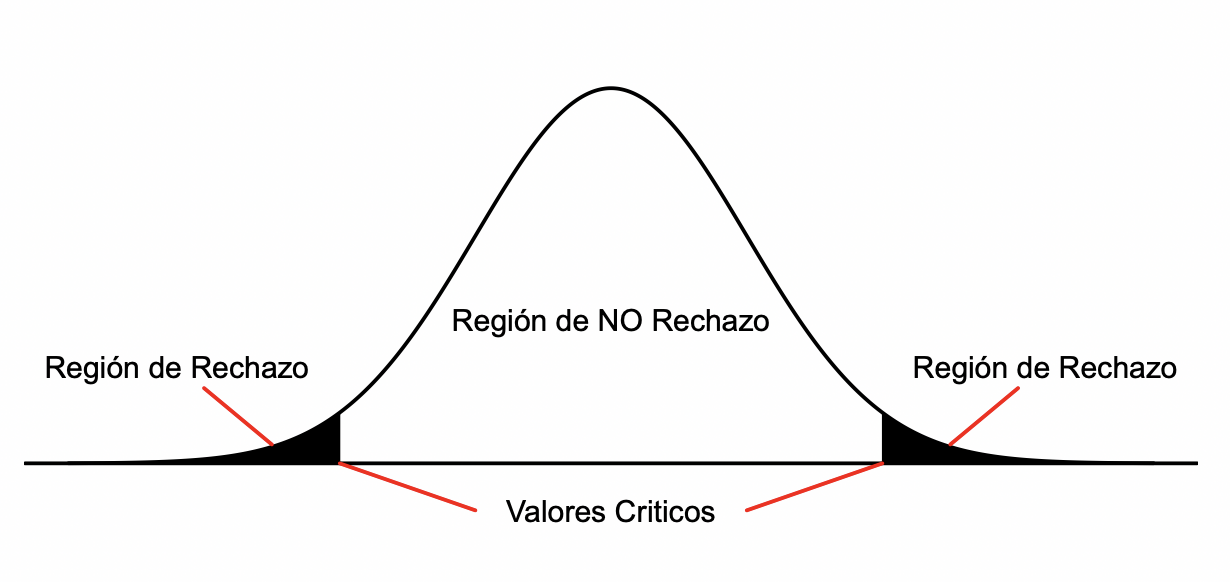
• Error Tipo I: Se rechaza $\mathrm{H}_0$ dado que era correcta. La probabilidad de Error Tipo I se denota como $\alpha$, la cual corresponde al nivel de significancia de la prueba de hipótesis.
• Error Tipo II: No se rechaza $\mathrm{H}_0$ dado que no era correcta. La probabilidad real de cometer Error Tipo I se conoce como valor-$p$.

Intervalos de confianza

Intervalos de confianza para la media

Sea $X_1, \ldots, X_n$ una muestra aleatoria de una población cuya distribución es $\operatorname{Normal}(\mu, \sigma)$.

Un estimador insesgado y consistente para $\mu$ esta dado por

$$\bar{X}_n=\frac{1}{n} \sum_{i=1}^n X_i \sim \operatorname{Normal}\left(\mu, \frac{\sigma}{\sqrt{n}}\right)$$

Intervalo de Confianza para $\mu$ con $\sigma$ conocido

Tenemos que

$$Z_n=\frac{\bar{X}_n-\mu}{\sigma / \sqrt{n}} \sim \operatorname{Normal}(0,1)$$

Luego, se puede mostrar que

$$<\mu>_{1-\alpha} \in \bar{X}_n \pm k_{1-\alpha / 2} \cdot \frac{\sigma}{\sqrt{n}}$$

Intervalo de Confianza para $\mu$ con $\sigma$ desconocido

Tenemos que

$$T_n=\frac{\bar{X}_n-\mu}{S / \sqrt{n}} \sim \mathrm{t} \text {-student }(n-1)$$

Luego, se puede mostrar que

$$<\mu>_{1-\alpha} \in \bar{X}_n \pm t_{1-\alpha / 2}(n-1) \cdot \frac{S}{\sqrt{n}}$$

Tamaño de la muestra

Como se aprecia en la construcción de los Intervalos de Confianza, el tamaño de muestra es fundamental.

Al observar el Intervalo de Confianza para $\mu$, se aprecia que el semiancho esta dado por:

$$k_{1-\alpha / 2} \frac{\sigma}{\sqrt{n}}=w$$

Lo anterior se conoce como Error de Estimación.

Por lo tanto, para una precisión $w$ dada, es posible determinar el tamaño de muestra necesaria, con $\sigma$ y $\alpha$ fijos, dado por

$$n=\left(\frac{k_{1-\alpha / 2} \sigma}{w}\right)^2$$

Nota

Alternativamente también se puede determinar un tamaño muestral a partir controlando por los errores tipo I y II de una prueba de hipótesis.

Intervalos de confianza para la varianza

Consideremos nuevamente una muestra aleatoria $X_1, \ldots, X_n$ proveniente de una población cuya distribución es $\operatorname{Normal}(\mu, \sigma)$.

Un estimador insesgado y consistente para $\sigma^2$ esta dado por:

$$S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}_n\right)^2 \Rightarrow \frac{(n-1) S^2}{\sigma^2} \sim \chi_{(n-1)}^2$$

Tenemos que

$$C_n=\frac{(n-1) S^2}{\sigma^2} \sim \chi_{(n-1)}^2$$

Luego, se puede mostrar que

$$<\sigma^2>_{1-\alpha} \in\left[\frac{(n-1) S^2}{c_{1-\alpha / 2}(n-1)} ; \frac{(n-1) S^2}{c_{\alpha / 2}(n-1)}\right]$$

Intervalos de confianza asintóticos

Sea $\hat{\theta}$ el estimador de máxima verosimilitud de un parámetro $\theta$. A partir del siguiente pivote

$$Z_n=\frac{\hat{\theta}-\theta}{\sqrt{\widehat{\operatorname{Var}(\hat{\theta})}}} \stackrel{\text { aprox }}{\sim} \operatorname{Normal}(0,1)$$

se tiene que

$$<\theta>_{1-\alpha} \in \hat{\theta} \pm k_{1-\alpha / 2} \cdot \sqrt{\widehat{\operatorname{Var}(\hat{\theta})}}$$

con $\operatorname{Var}(\hat{\theta})$ la varianza asintótica de $\hat{\theta}$.

Intervalos de confianza asintóticos: proporción

Por ejemplo, consideremos una muestra aleatoria $X_1, \ldots, X_n$ proveniente de una población cuya distribución es $\operatorname{Bernoulli}(p)$.

Un estimador insesgado y consistente para $p$ esta dado por:

$$\bar{X}_n=\frac{1}{n} \sum_{i=1}^n X_i \stackrel{\text { aprox. }}{\sim} \text { Normal }\left(p, \sqrt{\frac{p(1-p)}{n}}\right)$$

Tenemos que

$$Z_n=\frac{\bar{X}_n-p}{\sqrt{\frac{\bar{X}_n\left(1-\bar{X}_n\right)}{n}}} \stackrel{\text { aprox. }}{\sim} \operatorname{Normal}(0,1),$$

Luego,

$$<p>_{1-\alpha} \in \bar{X}_n \pm k_{1-\alpha / 2} \cdot \sqrt{\frac{\bar{X}_n\left(1-\bar{X}_n\right)}{n}}$$

Tests de bondad de ajuste

Test de Kolmogorov-Smirnov

Supongamos que queremos evaluar la calidad de ajuste del modelo $f_0(y)$.

$$\begin{aligned} H_0: f_Y(y) & =f_0(y) \quad \text { vs } \quad H_0: f_Y(y) \neq f_0(y) \\ d & =\max \left\{\left|F_n(y)-F_0(y)\right|\right\} \end{aligned}$$

con $F_n$ función de distribución acumulada empírica y $F_0$ función de distribución acumulada teórica del modelo que se quiere ajustar.

En R la función ks.test() realiza la comparación y calcula el valor $p$.

Test de Chi-Cuadrado

Considere una muestra de $n$ valores observados de una variable aleatoria y suponga una distribución de probabilidad subyacente. El test $\chi^2$ de bondad de ajuste compara las frecuencias observadas $O_1, O_2, \ldots, O_k$ de $k$ valores (o $k$ intervalos) de la variable con sus correspondientes frecuencias teóricas $E_1, E_2, \ldots, E_k$ que calculados suponiendo la distribución teórica.

Para evaluar la calidad del ajuste se usa el siguiente estadístico de prueba:

$$X^2=\sum_{i=1}^k \frac{\left(O_i-E_i\right)^2}{E_i}$$

cuya distribución se aproxima por una $\chi^2(k-1)$.

Si los parámetros de la distribución son desconocidos, estos deben ser estimados a partir de los datos y debe ser descontado de los grados de libertad de la distribución (por cada parámetro estimado). Si el estadístico de prueba $X^2>c_{1-\alpha}(f)$, la hipótesis nula que los datos provienen de la distribución escogida es rechazada.

El parámetro $f=(k-1)-\nu$, con $\nu$ el número de estadísticos necesarios para estimar los parámetros. Se recomienda aplicar este test cuando $k \geq 5$ y $E_i \geq 5$. En R la función chisq.test() realiza la comparación y calcula el valor-$p$ para el caso $\chi^2(k-1)$.

Regresión lineal

Introducción

La Inferencia vista anteriormente, puede ser abordada desde el punto de vista de Modelos Estadísticos. Así por ejemplo, si $Y_1, \ldots, Y_n$ es una muestra aleatoria de una distribución Normal con media $\mu$ y varianza $\sigma^2$ ambos parámetros desconocidos.

Este experimento se puede escribir en términos del siguiente modelo:

$$Y_i=\mu+\varepsilon_i \quad i=1, \ldots, n$$

donde $\varepsilon_i$ tienen distribución normal con media cero y varianza $\sigma^2$.

Al permitir que la media de $Y$ varíe de manera funcional con respecto a una covariable $X_i$ de la siguiente manera:

$$Y_i=\mu\left(X_i\right)+\varepsilon_i \quad i=1, \ldots, n$$

Obtenemos el modelo de regresión simple. Se llama a

$$y_i=\mathrm{E}\left(Y_i \mid x_i\right)=\mu\left(x_i\right)$$

a la curva de regresión de $Y$ sobre $x$. Si la relación funcional es lineal en los parámetros, es decir,

$$\mu\left(X_i\right)=\beta_0+\beta_1 X_i,$$

entonces el modelo se llama regresión lineal simple, y la curva de regresión esta dada por $y_i=\beta_0+\beta_1 x_i$.

En cambio si

$$\mu\left(X_i\right)=\beta_0 X_i^{\beta_1},$$

el modelo sería de regresión no lineal simple, y la curva de regresión esta dada por $y_i=\beta_0 x_i^{\beta_1}$.

Regresión lineal simple

Consideremos el modelo de regresión lineal simple,

$$Y_i=\beta_0+\beta_1 X_i+\varepsilon_i \quad i=1, \ldots, n$$

Algunos supuestos son:

1. Linealidad: La media condicional de $Y$ sobre $x$ es lineal

$$y=\mathrm{E}(Y \mid x)=\beta_0+\beta_1 x$$

2. Homocedasticidad: La varianza asociada a $f_{Y \mid x}(y)$ es la misma para todo $x$ e iguala $\sigma^2$.
3. Independencia: Las distribuciones condicionales son variables aleatorias independientes para todo $x$.
4. Normalidad: $f_{Y \mid x}(y)$ tiene distribución normal para todo $x$.

Regresión lineal simple bajo los supuestos dados

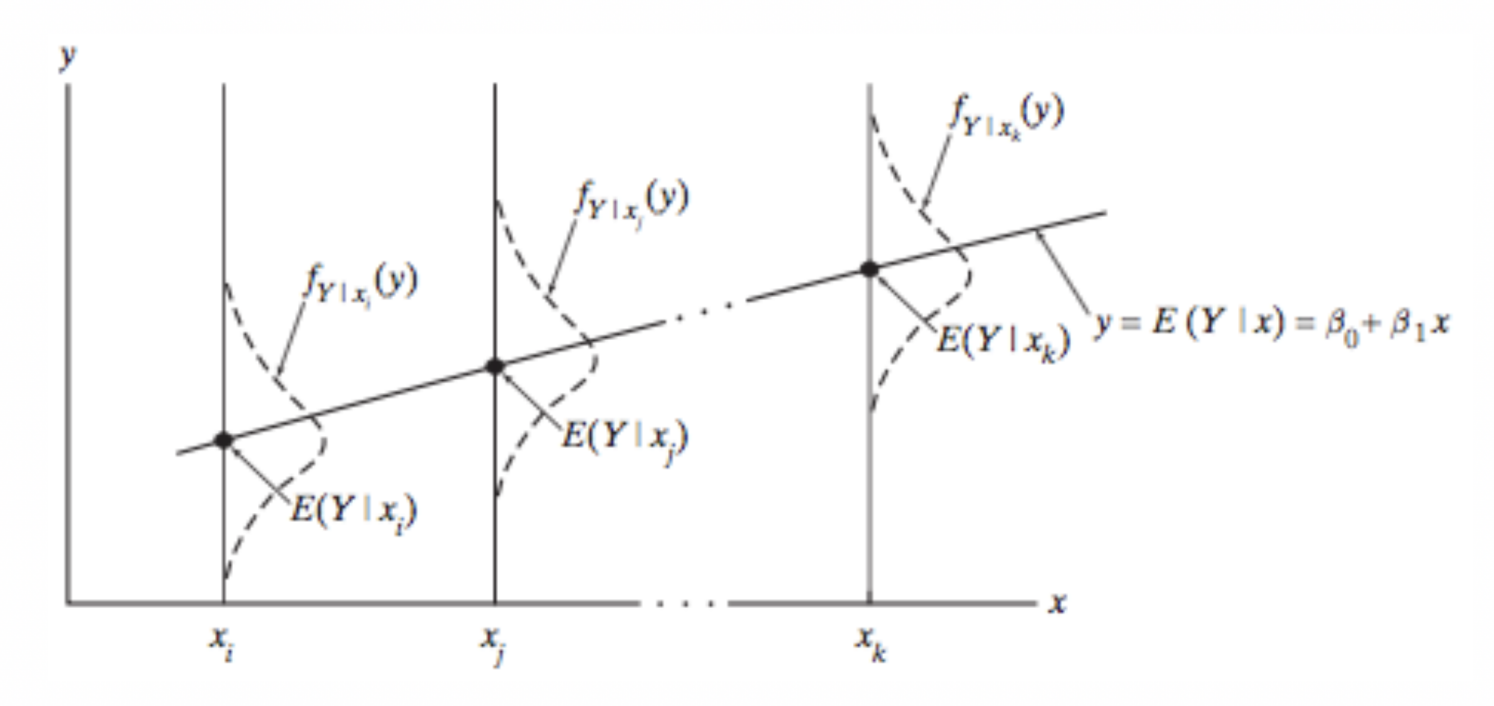
La interpretación de los parámetros del modelo son las siguientes:

• $\beta_0$ : intercepto, $\beta_0=\mathrm{E}(Y \mid X=0)$.
• $\beta_1$ : pendiente, corresponde a la variación de $\mathrm{E}(Y \mid X=x)$ cuando $x$ aumenta en una unidad.

Coeficiente de determinación

Coeficiente de determinación $R^2$:

$$R^2=\frac{S C R}{S C T}=\frac{\sum_{i=1}^n\left(y_i^{\prime}-\bar{y}\right)^2}{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}=1-\frac{S C E}{S C T}$$

Coeficiente de determinación $R^2$ ajustado:

$$r^2=1-\frac{s_{Y \mid x}^2}{s_Y^2}=1-\frac{(n-1)}{(n-2)} \frac{S C E}{S C T}=\bar{R}^2$$

Ambos se interpretan como la proporción de variación total que es explicada por el modelo de regresión lineal.

Test T y Test F

Los test T y test F son pruebas estadísticas utilizadas en el análisis de regresión lineal para evaluar la significancia de los parámetros estimados y el modelo en su conjunto, respectivamente.

El test T se usa para probar la hipótesis nula de que el coeficiente de una variable independiente en una regresión lineal es igual a cero (lo que implica que la variable no tiene efecto sobre la variable dependiente). La fórmula para el estadístico T es:

$$t = \frac{\hat{\beta}_j - 0}{SE(\hat{\beta}_j)}$$

Donde:

• $\hat{\beta}_j$ es el estimador del coeficiente de la variable independiente $j$.
• $SE(\hat{\beta}_j)$ es el error estándar del estimador $\hat{\beta}_j$.

La hipótesis nula ($H_0$) y la hipótesis alternativa ($H_a$) son:

• $H_0: \beta_j = 0$
• $H_a: \beta_j \neq 0$

Si el valor p asociado al estadístico T es menor que el nivel de significancia elegido (comúnmente 0.05), rechazamos la hipótesis nula, lo que sugiere que la variable independiente tiene un efecto significativo sobre la variable dependiente.

El test F se utiliza para probar la hipótesis nula de que un modelo de regresión lineal no tiene capacidad explicativa, es decir, que todos los coeficientes de las variables independientes son iguales a cero simultáneamente. Esto se hace comparando el modelo propuesto con un modelo más simple, usualmente el modelo que solo incluye el término de intercepción. La fórmula para el estadístico F es:

$$F = \frac{\frac{RSS_0 - RSS_1}{p}}{\frac{RSS_1}{n - p - 1}}$$

Donde:

• $RSS_0$ es la suma de cuadrados residuales del modelo restringido (solo con intercepción).
• $RSS_1$ es la suma de cuadrados residuales del modelo completo.
• $p$ es el número de parámetros estimados en el modelo completo excluyendo el término de intercepción.
• $n$ es el número total de observaciones.

La hipótesis nula ($H_0$) y la hipótesis alternativa ($H_a$) para el test F son:

• $H_0: \beta_1 = \beta_2 = \dots = \beta_p = 0$
• $H_a: \text{Al menos un } \beta_j \neq 0$

Si el valor p asociado al estadístico F es menor que el nivel de significancia elegido, rechazamos la hipótesis nula, lo que indica que el modelo en conjunto proporciona una mejor explicación de la variabilidad de la variable dependiente que el modelo sin ninguna de las variables independientes.

Ambos tests son fundamentales para entender la significancia de los coeficientes individuales y del modelo de regresión en su conjunto.