Álgebra lineal

Ecuaciones lineales en álgebra lineal

Operaciones elementales de fila

Las operaciones elementales de fila son tres operaciones que se pueden realizar en las filas de una matriz:

1. (Reemplazo) Sustituir una fila por la suma de sí misma y un múltiplo de otra fila.
2. (Intercambio) Intercambiar dos filas.
3. (Escalamiento) Multiplicar todos los elementos de una fila por una constante diferente de cero.

Forma escalonada de una matriz

Una matriz rectangular está en forma escalonada (o forma escalonada por filas) si tiene las siguientes tres propiedades:

1. Todas las filas diferentes de cero están arriba de las filas que solo contienen ceros.
2. Cada entrada principal de una fila está en una columna a la derecha de la entrada principal de la fila superior.
3. En una columna todas las entradas debajo de la entrada principal son ceros.

Si una matriz de forma escalonada satisface las siguientes condiciones adicionales, entonces está en forma escalonada reducida (o forma escalonada reducida por filas):

4. La entrada principal en cada fila diferente de cero es $1$.
5. Cada entrada principal $1$ es la única entrada distinta de cero en su columna.

Por ejemplo, las matrices

$$\left[\begin{array}{rrrc} 2 & -3 & 2 & 1 \\ 0 & 1 & -4 & 8 \\ 0 & 0 & 0 & 5 / 2 \end{array}\right] \text { y }\left[\begin{array}{llll} 1 & 0 & 0 & 29 \\ 0 & 1 & 0 & 16 \\ 0 & 0 & 1 & 3 \end{array}\right]$$

están en forma escalonada y forma escalonada reducida, respectivamente.

De forma general, las matrices en forma escalonada pueden tener entradas principales ($\small\blacksquare$) con cualquier valor diferente de cero, pero las entradas con asterisco ($*$) pueden tener cualquier valor, incluyendo cero.

$$\left[\begin{array}{llll} \small\blacksquare & * & * & * \\ 0 & \small\blacksquare & * & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]$$

En cambio, las matrices en forma escalonada reducida tienen entradas principales iguales a $1$ y hay ceros abajo y arriba de cada entrada principal $1$.

$$\left[\begin{array}{llll} 1 & 0 & * & * \\ 0 & 1 & * & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]$$

Unicidad de la forma escalonada reducida

Teorema

Cada matriz es equivalente por filas a una, y solo a una, matriz escalonada reducida.

Si una matriz $A$ es equivalente por filas a una matriz escalonada $U$, entonces $U$ se llama una forma escalonada (o una forma escalonada por filas) de $A$; si $U$ está en forma escalonada reducida, entonces $U$ es la forma escalonada reducida de $A$.

Posiciones pivote

Una posición pivote en una matriz $A$ es una ubicación en $A$ que corresponde a un $1$ principal en la forma escalonada reducida de $A$. Una columna pivote es una columna de $A$ que contiene una posición pivote.

En los ejemplos anteriores, los cuadrados ($\small\blacksquare$) identifican las posiciones pivote.

Algoritmo de reducción por filas

El algoritmo que sigue consta de cuatro pasos y produce una matriz en forma escalonada. Un quinto paso da por resultado una matriz en forma escalonada reducida.

1. Se inicia con la columna diferente de cero del extremo izquierdo. Esta es una columna pivote. La posición pivote se ubica en la parte superior.
2. Seleccione como pivote una entrada diferente de cero en la columna pivote. Si es necesario, intercambie filas para mover esta entrada a la posición pivote.
3. Utilice operaciones de remplazo de filas para crear ceros en todas las posiciones ubicadas debajo del pivote.
4. Cubra (o ignore) la fila que contiene la posición pivote y cubra todas las filas, si las hay, por encima de esta. Aplique los pasos 1 a 3 a la submatriz restante. Repita el proceso hasta que no haya filas diferentes de cero por modificar.
5. Empezando con la posición pivote del extremo derecho y trabajando hacia arriba y hacia la izquierda, genere ceros arriba de cada pivote. Si un pivote no es 1 , conviértalo en 1 mediante una operación de escalamiento.

La combinación de los pasos 1 a 4 se conoce como fase progresiva del algoritmo de reducción por filas. El paso 5, que produce la única forma escalonada reducida, se conoce como fase regresiva.

Ejemplo: Algoritmo de reducción por filas

Transforme la siguiente matriz a la forma escalonada, y luego a la forma escalonada reducida:

$$\left[\begin{array}{rrrrrr} 0 & 3 & -6 & 6 & 4 & -5 \\ 3 & -7 & 8 & -5 & 8 & 9 \\ 3 & -9 & 12 & -9 & 6 & 15 \end{array}\right]$$

Paso 1: Elegimos el pivote.

Paso 2: Intercambiamos las filas 1 y 3. (O bien, también se podrían intercambiar las filas 1 y 2).

Paso 3: Como paso preliminar, se podría dividir la fila superior entre el pivote, $3$. Pero con dos números $3$ en la columna 1, esto es tan fácil como sumar la fila 1 multiplicada por $-1$ a la fila 2.

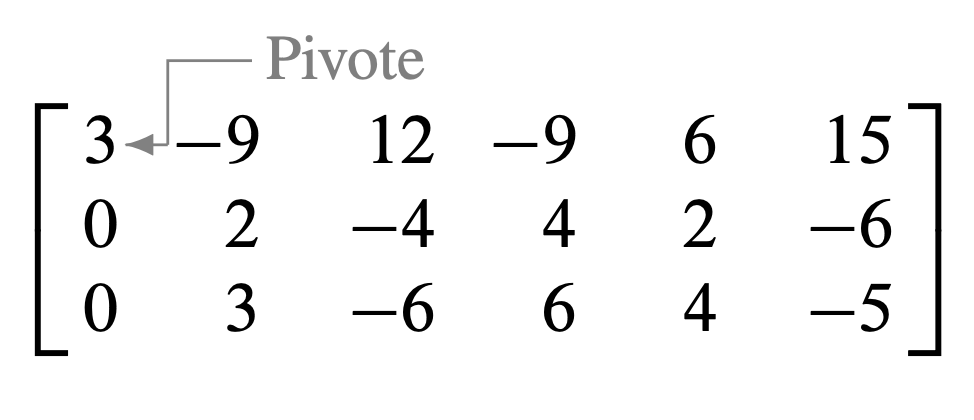
Paso 4: Con la fila 1 cubierta, el paso 1 muestra que la columna 2 es la próxima columna pivote; para el paso 2, seleccione como pivote la entrada "superior" en esa columna.

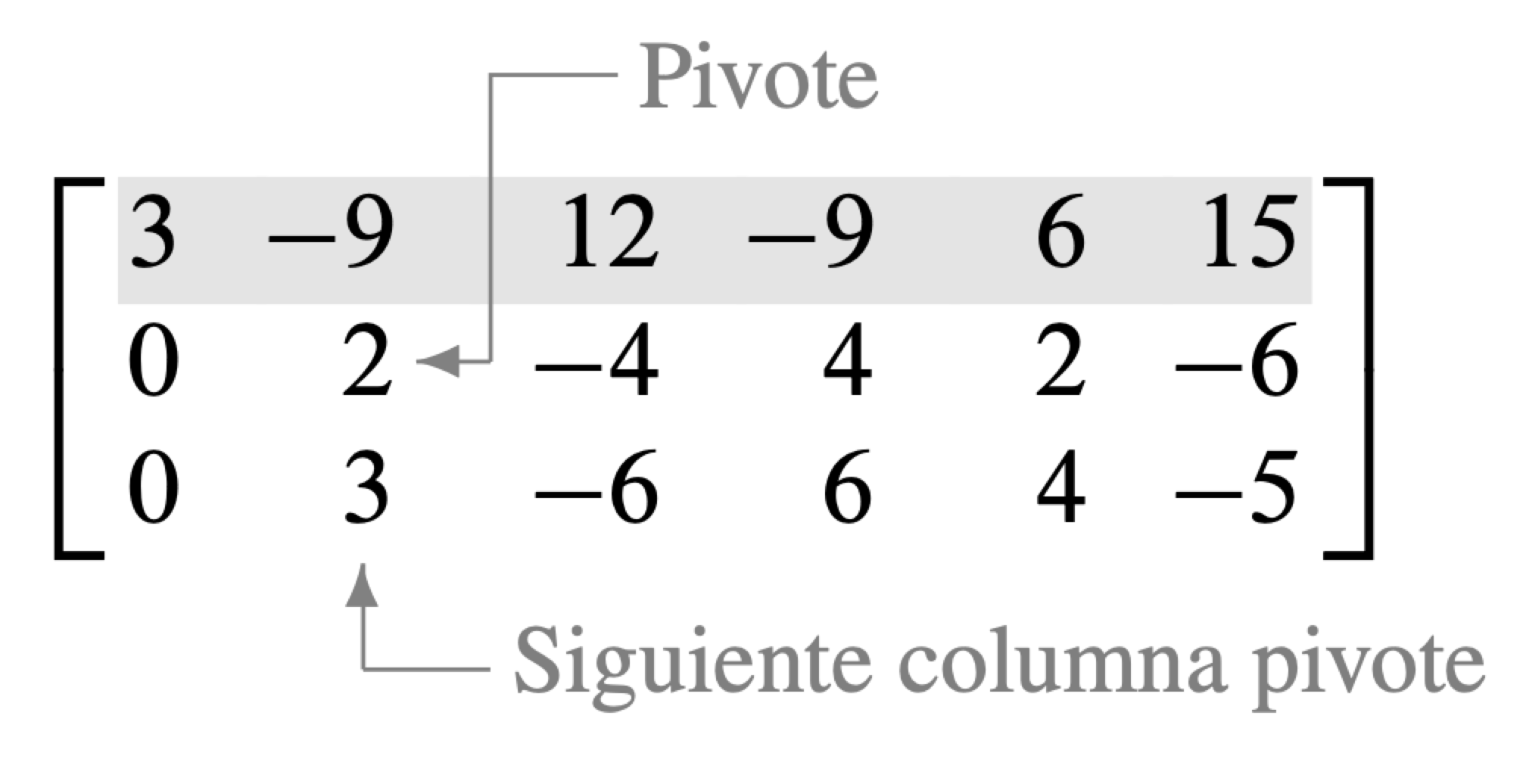
En el paso 3, se podría insertar un paso adicional de dividir la fila "superior" de la submatriz entre el pivote, $2$. En vez de ello, se suma la fila "superior" multiplicada por $-3 / 2$ a la fila de abajo. Esto produce

Para el paso 4, cuando se cubre la fila que contiene la segunda posición pivote, se obtiene una nueva submatriz con una sola fila:

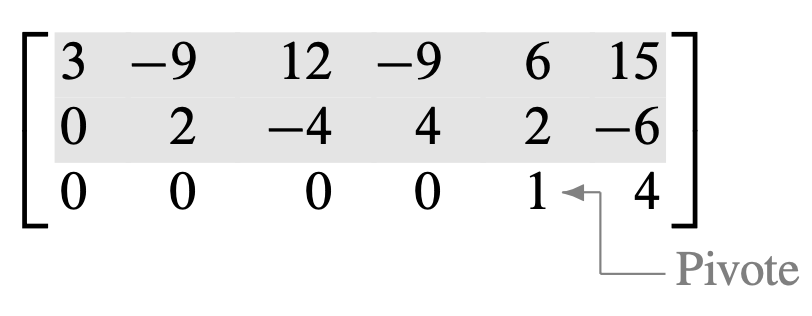
Los pasos 1 a 3 no necesitan aplicarse para esta submatriz, pues ya se ha alcanzado una forma escalonada para la matriz completa. Si se desea la forma escalonada reducida, se efectúa un paso más.

Paso 5: El pivote del extremo derecho está en la fila 3. Genere ceros sobre él, sumando múltiplos adecuados de la fila 3 a las filas 1 y 2.

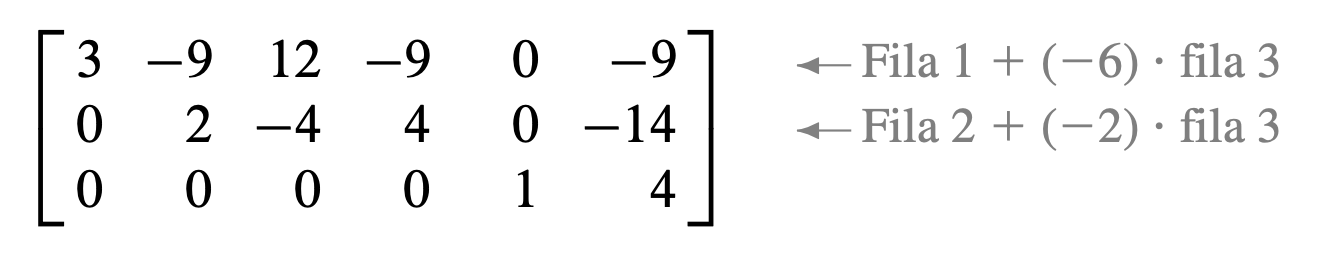
El siguiente pivote se encuentra en la fila 2 . Se escala esta fila dividiéndola entre el pivote.

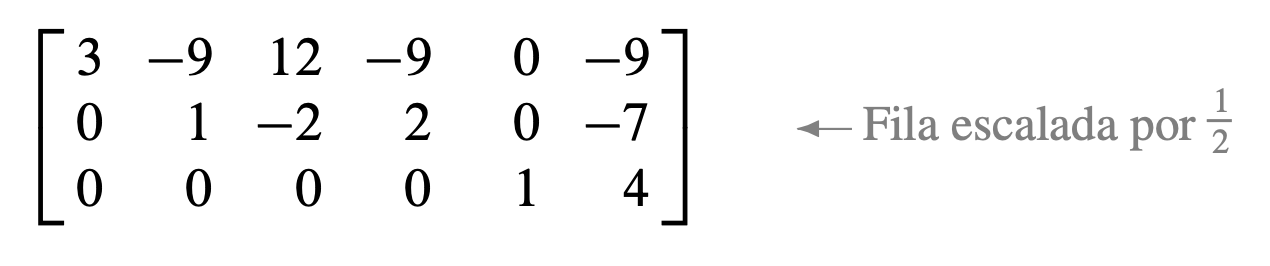
Cree un cero en la columna 2 sumando la fila 2 multiplicada por 9 a la fila 1.

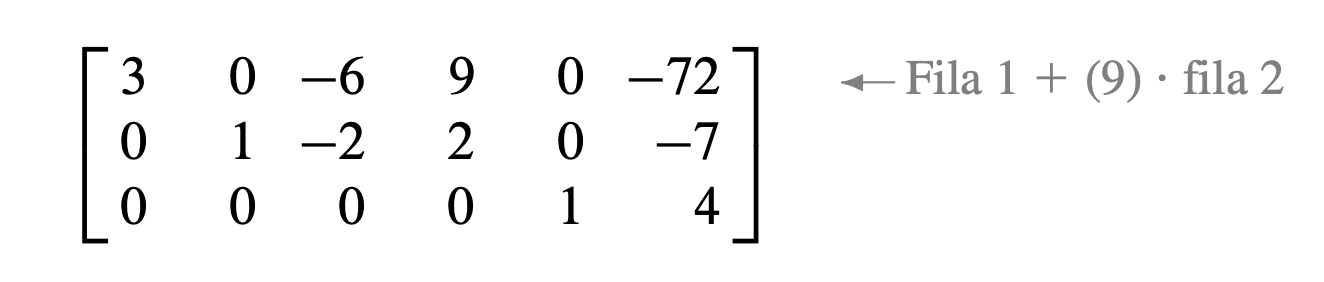
Finalmente, escale la fila 1 dividiéndola entre el pivote, 3.

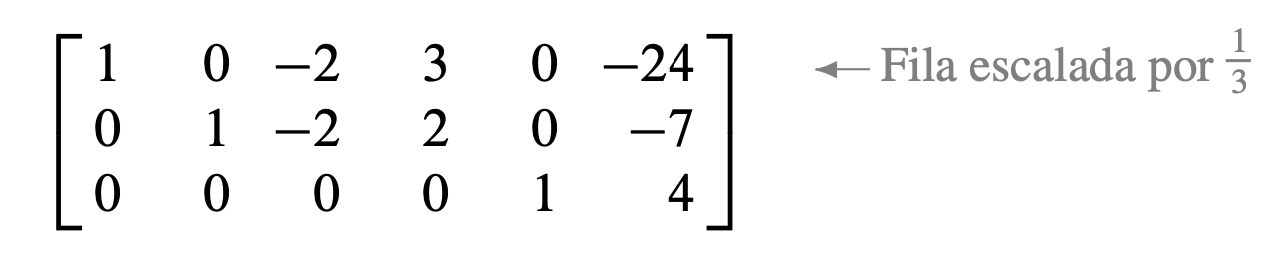
Esta es la forma escalonada reducida de la matriz original.

Soluciones de sistemas lineales

El algoritmo de reducción por filas conduce directamente a una descripción explícita del conjunto solución de un sistema lineal cuando se aplica a la matriz aumentada del sistema.

Suponga, por ejemplo, que la matriz aumentada de un sistema lineal se transformó a la forma escalonada reducida equivalente

$$\left[\begin{array}{rrrr}1 & 0 & -5 & 1 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 0 & 0\end{array}\right]$$

Existen tres variables porque la matriz aumentada tiene cuatro columnas. El sistema de ecuaciones asociado es

$$\begin{aligned} x_1-5 x_3 & =1 \\ x_2+x_3 & =4 \\ 0 & =0 \end{aligned}$$

Las variables $x_1$ y $x_2$ correspondientes a las columnas pivote se conocen como variables básicas. La otra variable, $x_3$, se denomina variable libre.

Siempre que un sistema es consistente, como el anterior, el conjunto solución se puede describir explícitamente al despejar en el sistema de ecuaciones reducido las variables básicas en términos de las variables libres. Esta operación es posible porque la forma escalonada reducida coloca a cada variable básica en una y solo una ecuación. En el sistema anterior, despeje $x_1$ de la primera ecuación y $x_2$ de la segunda. (Ignore la tercera ecuación, ya que no ofrece restricciones sobre las variables).

$$\left\{\begin{array}{l} x_1=1+5 x_3 \\ x_2=4-x_3 \\ x_3 \text { es libre } \end{array}\right.$$

El enunciado "$x_3$ es libre" significa que existe libertad de elegir cualquier valor para $x_3$. Una vez hecho esto, las fórmulas anteriores determinan los valores de $x_1$ y $x_2$. Por ejemplo, cuando $x_3=0$, la solución es $(1,4,0)$; cuando $x_3=1$, la solución es $(6,3,1)$. Cada asignación diferente de $x_3$ determina una solución (distinta) del sistema, y cada solución del sistema está determinada por una asignación de $x_3$.

Preguntas de existencia y unicidad

Teorema de existencia y unicidad

Un sistema lineal es consistente si y solo si la columna más a la derecha de la matriz aumentada no es una columna pivote, es decir, si y solo si una forma escalonada de la matriz aumentada no tiene filas del tipo

$$\left[\begin{array}{llll}0 & \cdots & 0 & b\end{array}\right] \quad \text{con } b \text{ diferente de cero}$$

Si un sistema lineal es consistente, entonces el conjunto solución contiene: i. una única solución, cuando no existen variables libres, o ii. una infinidad de soluciones, cuando hay al menos una variable libre.

El siguiente procedimiento indica cómo encontrar y describir todas las soluciones de un sistema lineal.

1. Escriba la matriz aumentada del sistema.
2. Emplee el algoritmo de reducción por filas para obtener una matriz aumentada equivalente en forma escalonada. Determine si el sistema es consistente o no. Si no existe solución, deténgase; en caso contrario, continúe con el siguiente paso.
3. Prosiga con la reducción por filas para obtener la forma escalonada reducida.
4. Escriba el sistema de ecuaciones correspondiente a la matriz obtenida en el paso 3.
5. Rescriba cada ecuación no nula del paso 4 de manera que su única variable básica se exprese en términos de cualquiera de las variables libres que aparecen en la ecuación.

Combinaciones lineales

Dados los vectores $\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_p$ en $\mathbb{R}^n$ y dados los escalares $c_1, c_2, \ldots, c_p$, el vector $\mathbf{y}$ definido por

$$\mathbf{y}=c_1 \mathbf{v}_1+\cdots+c_p \mathbf{v}_p$$

se llama combinación lineal de $\mathbf{v}_1, \ldots, \mathbf{v}_p$ con pesos $c_1, \ldots, c_p$.

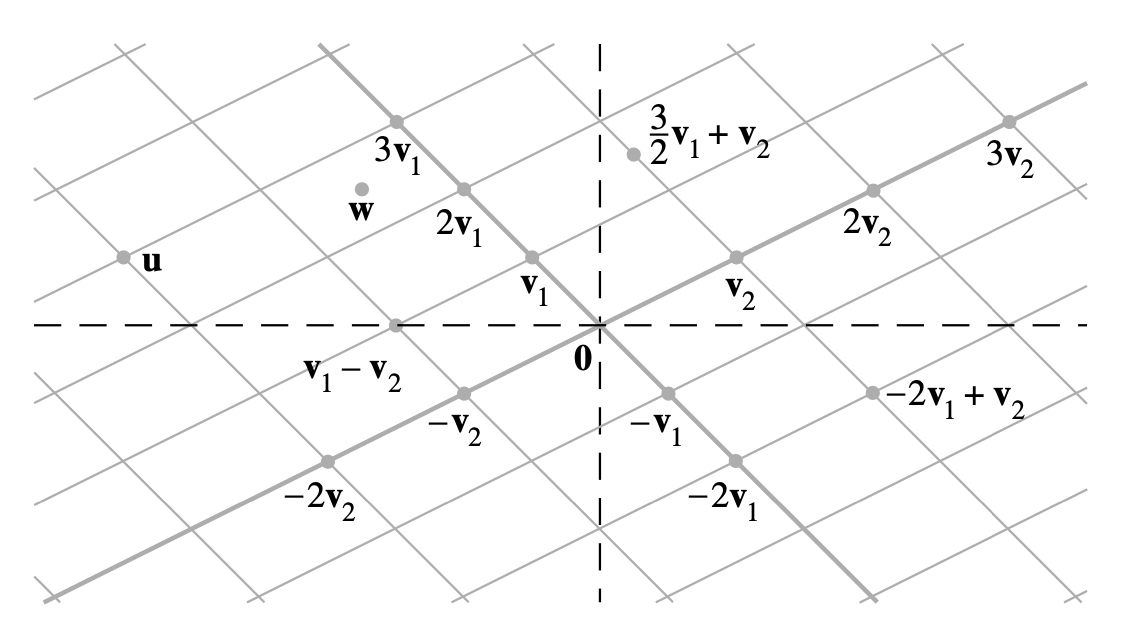
La siguiente figura identifica combinaciones lineales seleccionadas de $\mathbf{v}_1=\left[\begin{array}{r}-1 \\ 1\end{array}\right]$ y $\mathbf{v}_2=\left[\begin{array}{l}2 \\ 1\end{array}\right]$.

Ejemplo de combinación lineal

Espacio generado

Si $\mathbf{v}_1, \ldots, \mathbf{v}_p$ están en $\mathbb{R}^n$, entonces el conjunto de todas las combinaciones lineales de $\mathbf{v}_1, \ldots, \mathbf{v}_p$ se denota como $\text{Gen}\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ y se llama el subconjunto de $\mathbb{R}^n$ extendido o generado por $\mathbf{v}_1, \ldots, \mathbf{v}_p$. Es decir, $\text{Gen}\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ es el conjunto de todos los vectores que se pueden escribir en la forma

$$c_1 \mathbf{v}_1+c_2 \mathbf{v}_2+\cdots+c_p \mathbf{v}_p$$

con escalares $c_1, \ldots, c_p$.

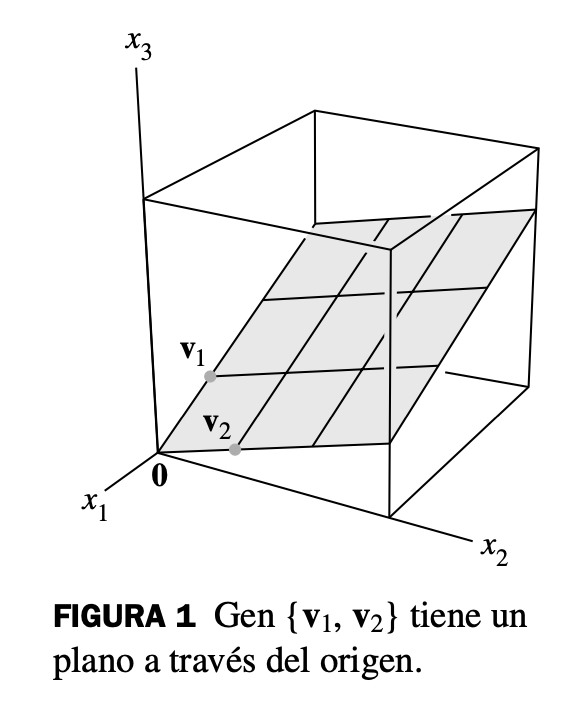
Sea $\mathbf{v}$ un vector diferente de cero en $\mathbb{R}^3$. Entonces $\text{Gen}\{\mathbf{v}\}$ es el conjunto de todos los múltiplos escalares de $\mathbf{v}$, que es el conjunto de puntos sobre la recta en $\mathbb{R}^3$ que pasa por $\mathbf{v}$ y $\mathbf{0}$.

Si $\mathbf{u}$ y $\mathbf{v}$ son vectores diferentes de cero en $\mathbb{R}^3$, y $\mathbf{v}$ no es un múltiplo de $\mathbf{u}$, entonces Gen $\{\mathbf{u}, \mathbf{v}\}$ es el plano en $\mathbb{R}^3$ que contiene a $\mathbf{u}, \mathbf{v}$ y $\mathbf{0}$. En particular, Gen $\{\mathbf{u}, \mathbf{v}\}$ contiene la recta en $\mathbb{R}^3$ que pasa por $\mathbf{u}$ y $\mathbf{0}$, y la recta que pasa por $\mathbf{v}$ y $\mathbf{0}$.

Espacio generado

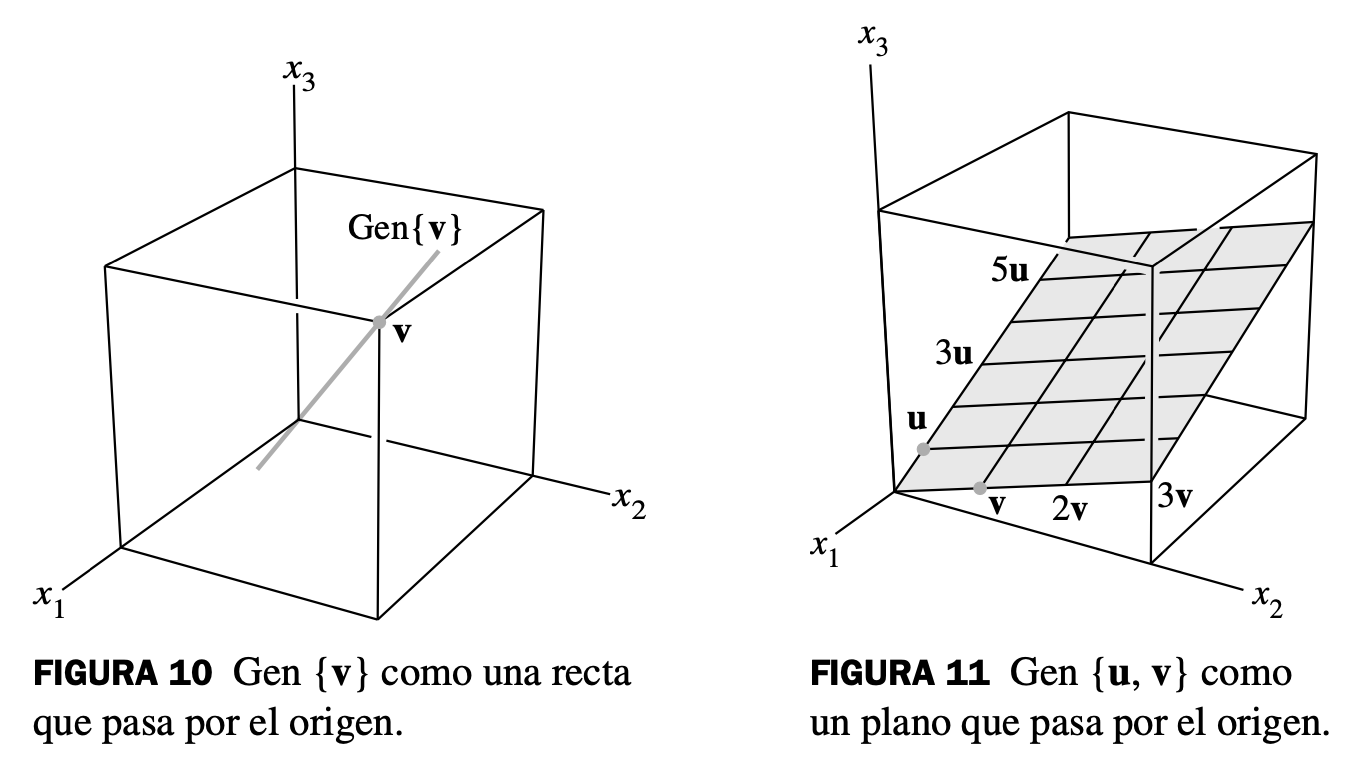
Ecuación matricial

Si $A$ es una matriz de $m \times n$, con columnas $\mathbf{a}_1, \ldots, \mathbf{a}_n$, y si $\mathbf{x}$ está en $\mathbb{R}^n$, entonces el producto de $A$ y $\mathbf{x}$, denotado como $A \mathbf{x}$, es la combinación lineal de las columnas de $A$ utilizando como pesos las entradas correspondientes en $\mathbf{x}$; es decir,

$$A \mathbf{x}=\left[\begin{array}{llll} \mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_n \end{array}\right]\left[\begin{array}{c} x_1 \\ \vdots \\ x_n \end{array}\right]=x_1 \mathbf{a}_1+x_2 \mathbf{a}_2+\cdots+x_n \mathbf{a}_n$$

Teorema

Si $A$ es una matriz de $m \times n$, con columnas $\mathbf{a}_1, \ldots, \mathbf{a}_n$, y si $\mathbf{b}$ está en $\mathbb{R}^m$, la ecuación matricial

$$A \mathbf{x}=\mathbf{b}$$

tiene el mismo conjunto solución que la ecuación vectorial

$$x_1 \mathbf{a}_1+x_2 \mathbf{a}_2+\cdots+x_n \mathbf{a}_n=\mathbf{b}$$

la cual, a la vez, tiene el mismo conjunto solución que el sistema de ecuaciones lineales cuya matriz aumentada es

$$\left[\begin{array}{lllll} \mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_n & \mathbf{b} \end{array}\right]$$

La definición de $A \mathbf{x}$ conduce directamente al siguiente hecho que resulta útil:

Existencia de solución

La ecuación $A \mathbf{x}=\mathbf{b}$ tiene una solución si y solo si b es una combinación lineal de las columnas de $A$.

Dado lo anterior, podemos enunciar el siguiente teorema:

Teorema

Sea $A$ una matriz de $m \times n$. Entonces, los siguientes enunciados son lógicamente equivalentes. Es decir, para una $A$ particular, todos los enunciados son verdaderos o todos son falsos.

• Para cada $\mathbf{b}$ en $\mathbb{R}^m$, la ecuación $A \mathbf{x}=\mathbf{b}$ tiene una solución.
• Cada $\mathbf{b}$ en $\mathbb{R}^m$ es una combinación lineal de las columnas de $A$.
• Las columnas de $A$ generan $\mathbb{R}^m$.
• $A$ tiene una posición pivote en cada fila.

Sistemas lineales homogéneos

Se dice que un sistema de ecuaciones lineales es homogéneo si se puede escribir en la forma $A \mathbf{x}=\mathbf{0}$, donde $A$ es una matriz de $m \times n$, y $\mathbf{0}$ es el vector cero en $\mathbb{R}^m$. Tal sistema $A \mathbf{x}=\mathbf{0}$ siempre tiene al menos una solución, a saber, $\mathbf{x}=\mathbf{0}$ (el vector cero en $\mathbb{R}^n$ ). Esta solución cero generalmente se conoce como solución trivial. Para una ecuación dada $A \mathbf{x}=\mathbf{0}$, la pregunta importante es si existe una solución no trivial, es decir, un vector $\mathbf{x}$ diferente de cero que satisfaga $A \mathbf{x}=\mathbf{0}$. El teorema de existencia y unicidad conduce de inmediato al siguiente resultado.

Resultado

La ecuación homogénea $A \mathbf{x}=\mathbf{0}$ tiene una solución no trivial si y solo si la ecuación tiene al menos una variable libre.

Independencia lineal

Las ecuaciones homogéneas se pueden estudiar desde una perspectiva diferente si las escribimos como ecuaciones vectoriales. De esta manera, la atención se transfiere de las soluciones desconocidas de $A \mathbf{x}=\mathbf{0}$ a los vectores que aparecen en las ecuaciones vectoriales.

Por ejemplo, considere la ecuación

$$x_1\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]+x_2\left[\begin{array}{l} 4 \\ 5 \\ 6 \end{array}\right]+x_3\left[\begin{array}{l} 2 \\ 1 \\ 0 \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right]$$

Esta ecuación tiene una solución trivial, desde luego, donde $x_1=x_2=x_3=0$. Al igual que hemos discutido antes, el asunto principal es si la solución trivial es la única.

Definición

Se dice que un conjunto indexado de vectores $\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ en $\mathbb{R}^n$ es linealmente independiente si la ecuación vectorial

$$x_1 \mathbf{v}_1+x_2 \mathbf{v}_2+\cdots+x_p \mathbf{v}_p=\mathbf{0}$$

solo tiene la solución trivial.

Se dice que el conjunto $\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ es linealmente dependiente si existen pesos $c_1, \ldots, c_p$, no todos cero, tales que

$$c_1 \mathbf{v}_1+c_2 \mathbf{v}_2+\cdots+c_p \mathbf{v}_p=\mathbf{0}$$

La ecuación que define el concepto de "linealmente dependiente" se llama relación de dependencia lineal entre $\mathbf{v}_1, \ldots, \mathbf{v}_p$ cuando no todos los pesos son cero. Un conjunto indexado es linealmente dependiente si y solo si no es linealmente independiente. Por brevedad, puede decirse que $\mathbf{v}_1, \ldots, \mathbf{v}_p$ son linealmente dependientes cuando queremos decir que $\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ es un conjunto linealmente dependiente. Se utiliza una terminología semejante para los conjuntos linealmente independientes.

Independencia lineal en columnas de una matriz

Suponga que, en vez de utilizar un conjunto de vectores, se inicia con una matriz $A=\left[\begin{array}{lll}\mathbf{a}_1 & \cdots & \mathbf{a}_n\end{array}\right]$. En tal caso, la ecuación matricial $A \mathbf{x}=\mathbf{0}$ se puede escribir como

$$x_1 \mathbf{a}_1+x_2 \mathbf{a}_2+\cdots+x_n \mathbf{a}_n=\mathbf{0}$$

Cada relación de dependencia lineal entre las columnas de A corresponde a una solución no trivial de $A \mathbf{x}=\mathbf{0}$. Así, tenemos el siguiente resultado importante.

Teorema

Las columnas de una matriz $A$ son linealmente independientes si y solo si la ecuación $A \mathbf{x}=\mathbf{0}$ tiene solo la solución trivial.

Geometría de la dependencia lineal

Siempre es posible determinar por inspección cuándo un conjunto de dos vectores es linealmente dependiente. Las operaciones de fila son innecesarias. Basta con comprobar si al menos uno de los vectores es un escalar multiplicado por el otro. (La prueba solo se aplica a conjuntos de dos vectores).

Dependencia lineal entre dos vectores

Un conjunto de dos vectores $\left\{\mathbf{v}_1, \mathbf{v}_2\right\}$ es linealmente dependiente si al menos uno de los vectores es un múltiplo del otro. El conjunto es linealmente independiente si y solo si ninguno de los vectores es un múltiplo del otro.

Dependencia lineal

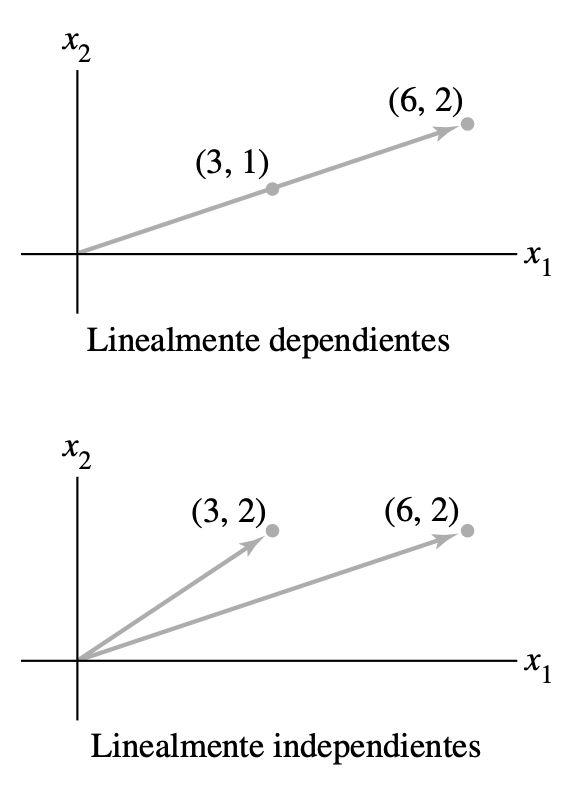
En términos geométricos, dos vectores son linealmente dependientes si y solo si ambos están sobre la misma recta que pasa por el origen.

Para dos o más vectores, tenemos el siguiente resultado:

Caracterización de conjuntos linealmente dependientes

Un conjunto indexado $S=\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ de dos o más vectores es linealmente dependiente si y solo si al menos uno de los vectores en $S$ es una combinación lineal de los otros. De hecho, si $S$ es linealmente dependiente y $\mathbf{v}_1 \neq \mathbf{0}$, entonces alguna $\mathbf{v}_j(\operatorname{con} j>1$ ) es una combinación lineal de los vectores precedentes, $\mathbf{v}_1, \ldots, \mathbf{v}_{j-1}$.

Los siguientes dos teoremas describen casos especiales en los cuales la dependencia lineal de un conjunto es automática.

Teorema

Si un conjunto contiene más vectores que entradas en cada vector, entonces el conjunto es linealmente dependiente. Es decir, cualquier conjunto $\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ en $\mathbb{R}^n$ es linealmente dependiente si $p>n$.

Teorema

Si un conjunto $S=\left\{\mathbf{v}_1, \ldots, \mathbf{v}_p\right\}$ en $\mathbb{R}^n$ contiene al vector cero, entonces el conjunto es linealmente dependiente.

Transformaciones lineales

La correspondencia de $\mathbf{x}$ a $A\mathbf{x}$ es una función de un conjunto de vectores a otro. Este concepto generaliza la noción común de una función como una regla que transforma un número real en otro.

Una transformación (o función o mapeo) $T$ de $\mathbb{R}^n$ a $\mathbb{R}^m$ es una regla que asigna a cada vector $\mathbf{x}$ en $\mathbb{R}^n$ un vector $T(\mathbf{x})$ en $\mathbb{R}^m$. El conjunto $\mathbb{R}^n$ se llama el dominio de $T$, y $\mathbb{R}^m$ se llama el codominio de $T$. La notación $T: \mathbb{R}^n \rightarrow \mathbb{R}^m$ indica que el dominio de $T$ es $\mathbb{R}^n$ y que el codominio es $\mathbb{R}^m$. Para $\mathbf{x}$ en $\mathbb{R}^n$, el vector $T(\mathbf{x})$ en $\mathbb{R}^m$ es la imagen de $\mathbf{x}$ (bajo la acción de $T$ ). El conjunto de todas las imágenes $T(\mathbf{x})$ es el rango de $T$.

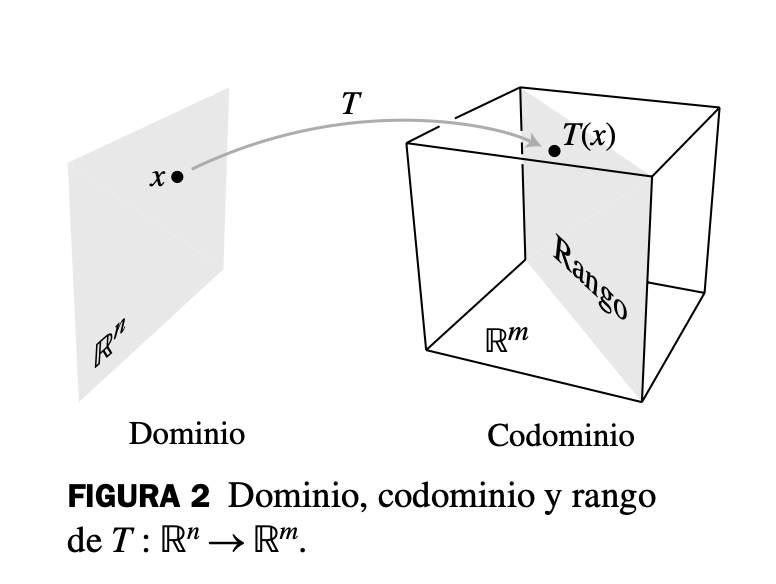
Para cada $\mathbf{x}$ en $\mathbb{R}^n, T(\mathbf{x})$ se calcula como $A \mathbf{x}$, donde $A$ es una matriz de $m \times n$. Para simplificar, algunas veces esta transformación matricial se denota como $\mathbf{x} \mapsto A \mathbf{x}$. Observe que el dominio de $T$ es $\mathbb{R}^n$ cuando $A$ tiene $n$ columnas, y el codominio de $T$ es $\mathbb{R}^m$ cuando cada columna de $A$ tiene $m$ entradas. El rango de $T$ es el conjunto de todas las combinaciones lineales de las columnas de $A$, porque cada imagen $T(\mathbf{x})$ es de la forma $A \mathbf{x}$.

Definición

Una transformación (o mapeo) $T$ es lineal si:

• $T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v})$ para todas las $\mathbf{u}$, $\mathbf{v}$ en el dominio de $T$;
• $T(c \mathbf{u})=c T(\mathbf{u})$ para todos los escalares $c$ y para todas las $\mathbf{u}$ en el dominio de $T$.

Álgebra de matrices

Operaciones básicas

Sean $A, B$ y $C$ matrices del mismo tamaño, y sean $r$ y $s$ escalares.

• $A+B=B+A$
• $r(A+B)=r A+r B$
• $(A+B)+C=A+(B+C)$
• $(r+s) A=r A+s A$
• $A+0=A$
• $r(s A)=(r s) A$
• $A^k=\underbrace{A \cdots A}_k$

Multiplicación de matrices

Si $A$ es una matriz de $m \times n$, y si $B$ es una matriz de $n \times p$ con columnas $\mathbf{b}_1, \ldots, \mathbf{b}_p$ entonces el producto $A B$ es la matriz de $m \times p$ cuyas columnas son $A \mathbf{b}_1, \ldots, A \mathbf{b}_p$. Es decir,

$$A B=A\left[\begin{array}{llll} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_p \end{array}\right]=\left[\begin{array}{llll} A \mathbf{b}_1 & A \mathbf{b}_2 & \cdots & A \mathbf{b}_p \end{array}\right]$$

Es decir, cada columna de $A B$ es una combinación lineal de las columnas de $A$ usando pesos de la columna correspondiente de $B$.

Regla fila-columna para calcular AB

Si el producto $A B$ está definido, entonces la entrada en la fila $i$ y la columna $j$ de $A B$ es la suma de los productos de las entradas correspondientes de la fila $i$ de $A$ y la columna $j$ de $B$. Si $(A B)_{i j}$ denota la entrada $(i, j)$ en $A B$, y si $A$ es una matriz de $m \times n$, entonces

$$(A B)_{i j}=a_{i 1} b_{1 j}+a_{i 2} b_{2 j}+\cdots+a_{i n} b_{n j}$$

Propiedades de la multiplicación de matrices

Sea $A$ una matriz de $m \times n$, y sean $B$ y $C$ matrices con tamaños para los que las sumas y los productos indicados están definidos.

• $A(B C)=(A B) C$
• $A(B+C)=A B+A C$
• $(B+C) A=B A+C A$
• $r(A B)=(r A) B=A(r B)$ para cualquier escalar $r$
• $I_m A=A=A I_n$

Advertencias

1. En general, $A B \neq B A$.
2. Las leyes de la cancelación no se aplican en la multiplicación de matrices. Es decir, si $A B=A C$, en general no es cierto que $B=C$.
3. Si un producto $A B$ es la matriz cero, en general, no se puede concluir que $A=0$ o $B=0$.

La transpuesta de una matriz

Dada una matriz $A$ de $m \times n$, la transpuesta de $A$ es la matriz de $n \times m$, que se denota con $A^T$, cuyas columnas se forman a partir de las filas correspondientes de $A$.

Teorema

Sean $A$ y $B$ matrices cuyos tamaños son adecuados para las siguientes sumas y productos.

• $\left(A^T\right)^T=A$
• $(A+B)^T=A^T+B^T$
• Para cualquier escalar $r,(r A)^T=r A^T$
• $(A B)^T=B^T A^T$

Inversa de una matriz

Se dice que una matriz $A$ de $n \times n$ es invertible si existe otra matriz $A^{-1}$ de $n \times n$ tal que

$$A^{-1} A=I \quad \text { y } \quad A A^{-1}=I$$

donde $I=I_n$, la matriz identidad de $n \times n$. En este caso, $A^{-1}$ es una inversa de $A$.

Teorema

Sea $A=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$. Si $a d-b c \neq 0$, entonces $A$ es invertible y

$$A^{-1}=\frac{1}{\text{det}(A)}\left[\begin{array}{rr} d & -b \\ -c & a \end{array}\right]$$

Si $\text{det}(A)=a d-b c=0$, entonces $A$ no es invertible.

La definición de matriz inversa nos entrega el siguiente teorema:

Teorema

Si $A$ es una matriz invertible de $n \times n$, entonces, para cada $\mathbf{b}$ en $\mathbb{R}^n$, la ecuación $A \mathbf{x}=\boldsymbol{b}$ tiene la solución única $\mathbf{x}=A^{-1} \mathbf{b}$.

Además, podemos definir las siguientes propiedades para matrices invertibles:

• Si $A$ es una matriz invertible, entonces $A^{-1}$ es invertible y $$\left(A^{-1}\right)^{-1}=A$$
• Si $A$ y $B$ son matrices invertibles de $n \times n$, entonces también lo es $A B$, y la inversa de $A B$ es el producto de las inversas de $A$ y $B$ en el orden opuesto. Es decir, $$(A B)^{-1}=B^{-1} A^{-1}$$
• Si $A$ es una matriz invertible, también lo es $A^T$, y la inversa de $A^T$ es la transpuesta de $A^{-1}$. Es decir, $$\left(A^T\right)^{-1}=\left(A^{-1}\right)^T$$

Matrices elementales

Una matriz elemental es aquella que se obtiene al realizar una única operación elemental de fila sobre una matriz identidad. El siguiente ejemplo ilustra los tres tipos de matrices elementales.

Si se realiza una operación elemental de fila con una matriz $A$ de $m \times n$, la matriz resultante se puede escribir como $E A$, donde la matriz $E$ de $m \times m$ se crea al realizar la misma operación de fila sobre $I_m$.

Por ejemplo, si

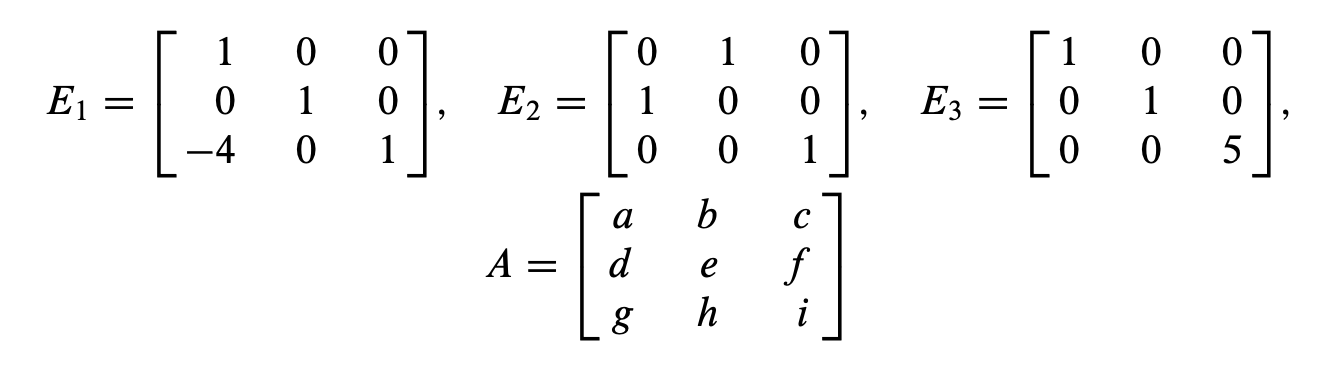
entonces

Al sumar a la fila 3 la fila 1 de $A$ multiplicada por $-4$ , se obtiene $E_1 A$. (Esta es una operación de remplazo de filas). Con un intercambio de las filas 1 y 2 de $A$ se obtiene $E_2 A$, y multiplicando la fila 3 de $A$ por $5$ se obtiene $E_3 A$.

Teorema

Toda matriz elemental $E$ es invertible. La inversa de $E$ es la matriz elemental del mismo tipo que transforma a $E$ de nuevo en $I$.

Una matriz $A$ de $n \times n$ es invertible si y solo si $A$ es equivalente por filas a $I_n$, y, en este caso, cualquier secuencia de operaciones elementales de fila que reduzca $A$ a $I_n$ también transforma a $I_n$ en $A^{-1}$.

El teorema anterior nos da el siguiente algoritmo para determinar la inversa de una matriz $A$ de $n \times n$:

Algoritmo para determinar la inversa de una matriz

Reduzca por filas la matriz aumentada $\left[\begin{array}{ll}A & I\end{array}\right]$. Si $A$ es equivalente por filas a $I$, entonces $\left[\begin{array}{ll}A & I\end{array}\right]$ es equivalente por filas a $\left[\begin{array}{ll}I & A^{-1}\end{array}\right]$. De otra manera, $A$ no tiene inversa.

El teorema de la matriz invertible

El resultado principal de todo el estudio anterior es el siguiente teorema.

Teorema

Sea $A$ una matriz cuadrada de $n \times n$. Entonces, los siguientes enunciados son equivalentes. Es decir, para una $A$ dada, los enunciados son todos ciertos o todos falsos.

• $A$ es una matriz invertible.
• $A$ es equivalente por filas a la matriz identidad de $n \times n$.
• $A$ tiene $n$ posiciones pivote.
• La ecuación $A \mathbf{x}=\mathbf{0}$ tiene solamente la solución trivial.
• Las columnas de $A$ forman un conjunto linealmente independiente.
• La transformación lineal $\mathbf{x} \mapsto A \mathbf{x}$ es uno a uno.
• La ecuación $A \mathbf{x}=\mathbf{b}$ tiene al menos una solución para toda $\mathbf{b}$ en $\mathbb{R}^n$.
• Las columnas de $A$ generan $\mathbb{R}^n$.
• La transformación lineal $\mathbf{x} \mapsto A \mathbf{x}$ mapea $\mathbb{R}^n$ sobre $\mathbb{R}^n$.
• Existe una matriz $C$ de $n \times n$ tal que $C A=I$,
• Existe una matriz $D$ de $n \times n$ tal que $A D=I$.
• $A^T$ es una matriz invertible.

Transformación lineal invertible

Se dice que una transformación lineal $T: \mathbb{R}^n \rightarrow \mathbb{R}^n$ es invertible si existe una función $S: \mathbb{R}^n \rightarrow \mathbb{R}^n$ tal que

$$\begin{array}{ll} S(T(\mathbf{x}))=\mathbf{x} & \text { para toda } \mathbf{x} \text { en } \mathbb{R}^n \\ T(S(\mathbf{x}))=\mathbf{x} & \text { para toda } \mathbf{x} \text { en } \mathbb{R}^n \end{array}$$

El siguiente teorema establece que si dicha $S$ existe, es única y debe ser una transformación lineal. Se dice que $S$ es la inversa de $T$ y se escribe como $T^{-1}$.

Teorema

Sea $T: \mathbb{R}^n \rightarrow \mathbb{R}^n$ una transformación lineal y sea $A$ la matriz estándar para $T$. Así, $T$ es invertible si y solo si $A$ es una matriz invertible. En tal caso, la transformación lineal $S$ dada por $S(\mathbf{x})=A^{-1} \mathbf{x}$ es la única función que satisface las ecuaciones mostradas.

Subespacios

Un subespacio de $\mathbb{R}^n$ es cualquier conjunto $H$ en $\mathbb{R}^n$ que tenga tres propiedades:

• El vector cero está en $H$.
• Para cada $\mathbf{u}$ y $\mathbf{v}$ en $H$, la suma $\mathbf{u}+\mathbf{v}$ está en $H$.
• Para cada $\mathbf{u}$ en $H$ y cada escalar $c$, el vector $c \mathbf{u}$ está en $H$.

Dicho con palabras, un subespacio es cerrado bajo la suma y la multiplicación escalar.

Espacio de columnas

Los subespacios de $\mathbb{R}^n$ generalmente se presentan en aplicaciones y en la teoría en una de dos formas. En ambos casos, es posible relacionar el subespacio con una matriz.

Definición

El espacio de columnas de una matriz $A$ es el conjunto $\mathrm{Col} A$ de todas las combinaciones de las columnas de $A$.

Si $A=\left[\begin{array}{lll}\mathbf{a}_1 & \cdots & \mathbf{a}_n\end{array}\right]$, con las columnas en $\mathbb{R}^m$, entonces $\text{Col} A$ es lo mismo que $\text{Gen}\left\{\mathbf{a}_1, \ldots, \mathbf{a}_n\right\}$. De hecho, el espacio columna de una matriz de $\boldsymbol{m} \times \boldsymbol{n}$ es un subespacio de $\mathbb{R}^m$. Observe que $\text{Col} A$ es igual a $\mathbb{R}^m$ solo cuando las columnas de $A$ generan a $\mathbb{R}^m$. Si no la generan, $\text{Col}A$ es solo una parte de $\mathbb{R}^m$.

Cuando un sistema de ecuaciones lineales está escrito en la forma $A \mathbf{x}=\mathbf{b}$, el espacio columna de $A$ es el conjunto de todas las $\mathbf{b}$ para las que el sistema tiene una solución.

Espacio nulo

El espacio nulo de una matriz $A$ es el conjunto $\mathrm{Nul} A$ de todas las soluciones posibles para la ecuación homogénea $A \mathbf{x}=\mathbf{0}$.

Cuando $A$ tiene $n$ columnas, las soluciones de $A \mathbf{x}=\mathbf{0}$ pertenecen a $\mathbb{R}^n$, y el espacio nulo de $A$ es un subconjunto de $\mathbb{R}^n$. De hecho, Nul $A$ tiene las propiedades de un subespacio de matrices de $\mathbb{R}^n$.

Teorema

El espacio nulo de una matriz $A$ de $m \times n$ es un subespacio de $\mathbb{R}^n$. De manera equivalente, el conjunto de todas las soluciones posibles para un sistema $A \mathbf{x}=\mathbf{0}$ de $m$ ecuaciones lineales homogéneas con $n$ incógnitas es un subespacio de $\mathbb{R}^n$.

Base para un subespacio

Como, por lo general, un subespacio contiene un número infinito de vectores, algunos problemas relacionados con subespacios se manejan mejor trabajando con un conjunto finito y pequeño de vectores que genere el subespacio. Cuanto menor sea el conjunto, será mejor. Es factible demostrar que el conjunto generador más pequeño posible debe ser linealmente independiente.

Definición

Una base de un subespacio $H$ de $\mathbb{R}^n$ es un conjunto linealmente independiente en $H$, que genera a $H$.

La base estándar para todo el espacio

warning

Solo son 4 preguntas de Lineal, después me sigo pegando el show terminando esto 😢