Cinemática

Movimiento rectilíneo

Velocidad media

Si elegimos un eje, por ejemplo la componente $x$ de la velocidad promedio, o velocidad media, es la componente $x$ del desplazamiento, $\Delta x$, dividida entre el intervalo de tiempo $\Delta t$ en el que ocurre el desplazamiento. Usamos el símbolo $v_{\text {med- } x}$ para representar velocidad media (el subíndice "med" indica que se trata de un valor promedio y el subíndice $x$ indica que ésta es la componente $x$):

$$v_{\text {med- } x}=\frac{x_2-x_1}{t_2-t_1}=\frac{\Delta x}{\Delta t}$$

Nota

Hay algunas reglas sencillas para la velocidad media. Siempre que $\boldsymbol{x}$ sea positiva y aumente o sea negativa y se vuelva menos negativa, la partícula se mueve en la dirección $+\boldsymbol{x}$ y $\boldsymbol{v}_{\text {med-x }}$ es positiva. Siempre que $x$ sea positiva y disminuya, o sea negativa y se vuelva más negativa, la partícula se mueve en la dirección $-\boldsymbol{x}$ y $\boldsymbol{v}_{\text {med- } x}$ es negativa.

Velocidad instantánea

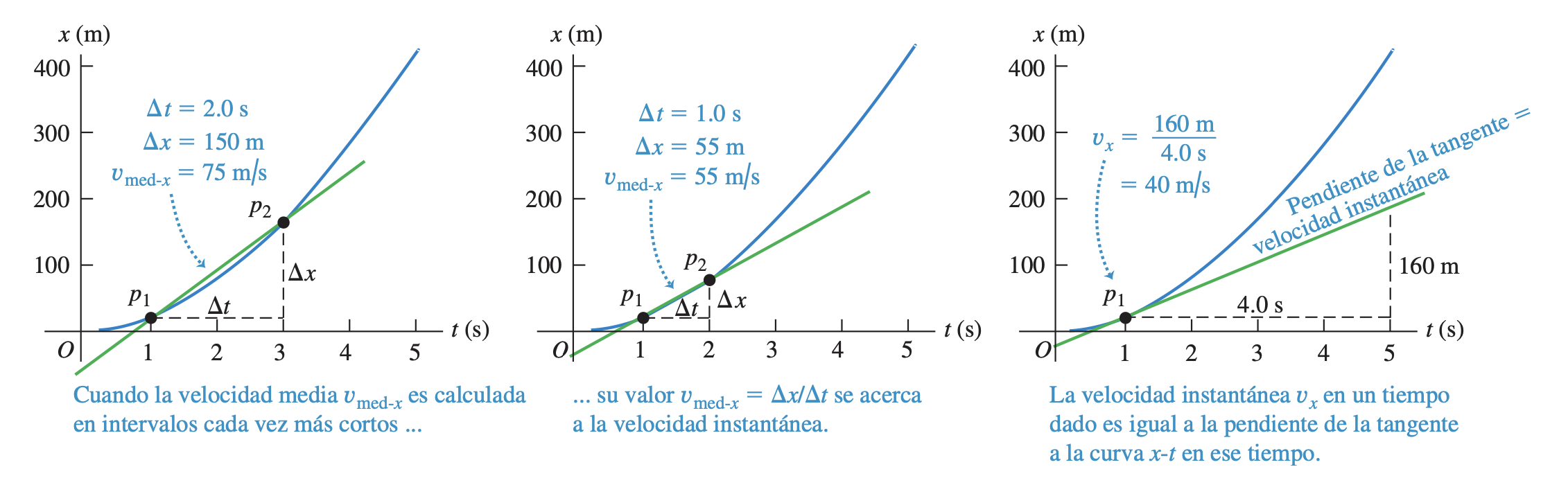
La velocidad instantánea es el límite de la velocidad media conforme el intervalo de tiempo se acerca a cero; es igual a la tasa instantánea de cambio de posición con el tiempo. Usamos el símbolo $v_x$, sin "med" en el subíndice, para la velocidad instantánea en el eje $x$:

$$v_x=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t}$$

Nota

En una gráfica de posición en función del tiempo para movimiento rectilíneo, la velocidad instantánea en cualquier punto es igual a la pendiente de la tangente a la curva en ese punto.

Aceleración media e instantánea

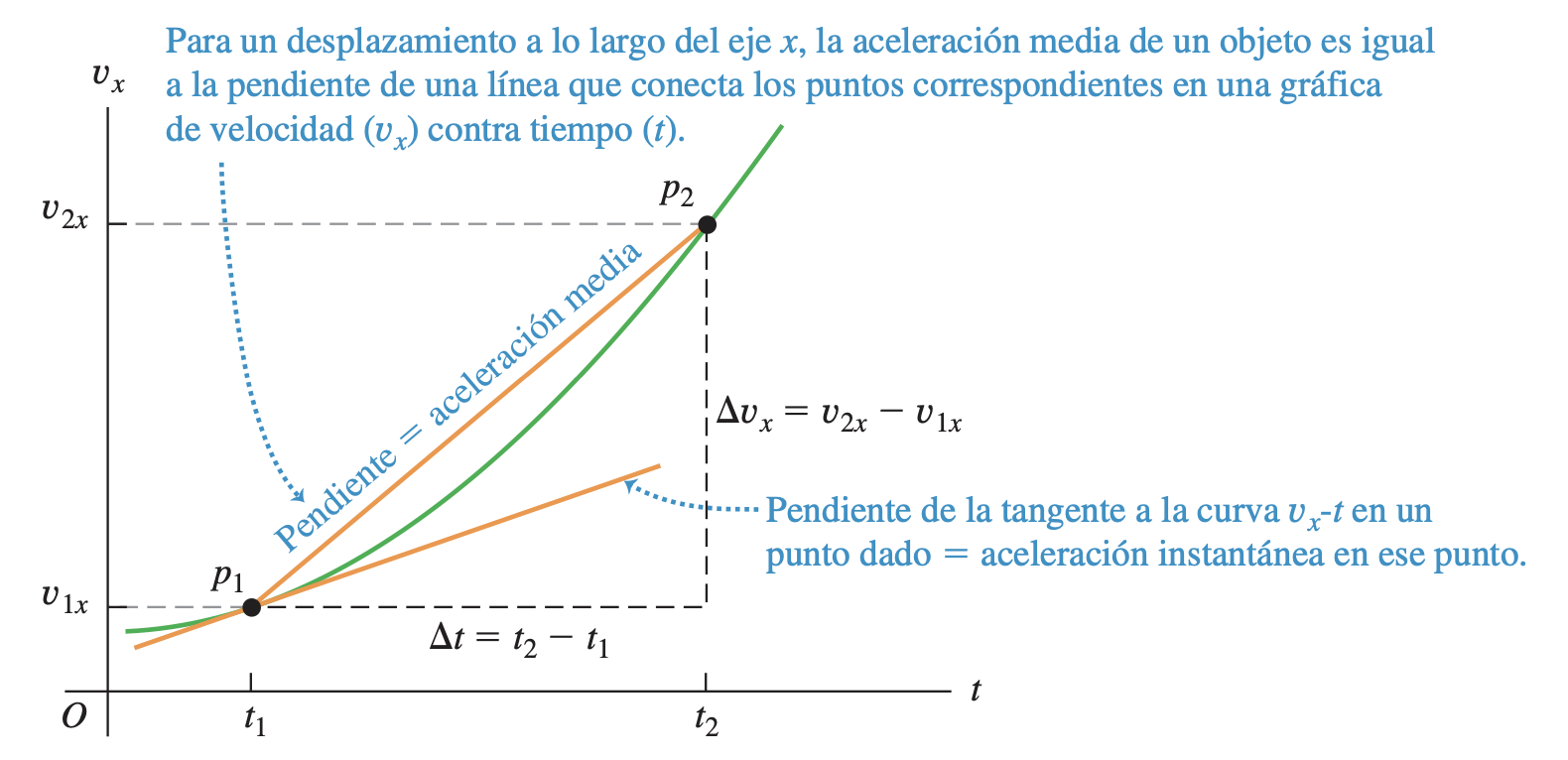
Consideremos otra vez el movimiento de una partícula en el eje $x$. Suponga que, en el tiempo $t_1$, la partícula está en el punto $P_1$ y tiene una componente $x$ de velocidad (instantánea) $v_{1 x}$, y en un instante posterior $t_2$ está en $P_2$ y tiene una componente $x$ de velocidad $v_{2 x}$. Así, la componente $x$ de la velocidad cambia en $\Delta v_x=v_{2 x}-v_{1 x}$ en el intervalo $\Delta t=t_2-t_1$.

Definimos la aceleración media de la partícula al moverse de $P_1$ a $P_2$ como una cantidad vectorial cuya componente $x$ es $a_{\text {med- } x}$ igual a $\Delta v_x$, el cambio en la componente $x$ de la velocidad, dividido entre el intervalo de tiempo $\Delta t$ :

$$a_{\text {med- } x}=\frac{v_{2 x}-v_{1 x}}{t_2-t_1}=\frac{\Delta v_x}{\Delta t}$$

En cambio, la aceleración instantánea es el límite de la aceleración media conforme el intervalo de tiempo se acerca a cero. En el lenguaje del cálculo, la aceleración instantánea es la tasa instantánea de cambio de la velocidad con el tiempo. Así,

$$a_x=\lim _{\Delta t \rightarrow 0} \frac{\Delta v_x}{\Delta t}=\frac{d v_x}{d t}$$

Nota

En una gráfica de velocidad en función del tiempo, la aceleración instantánea en cualquier punto es igual a la pendiente de la tangente de la curva en ese punto.

Movimiento con aceleración constante

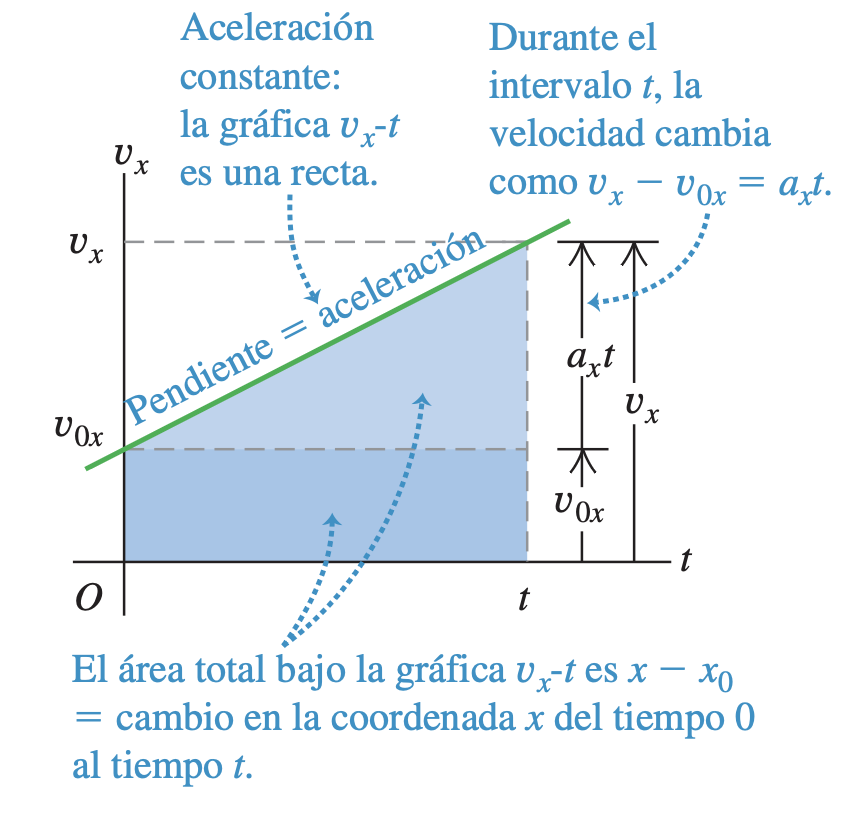
Cuando la aceleración $a_x$ es constante, la aceleración media $a_{\text {med- } x}$ para cualquier intervalo es $a_x$. Esto vuelve sencillo derivar las ecuaciones para la posición $x$ y la velocidad $v_x$ como funciones del tiempo. Para encontrar una expresión para $v_x$ primero sustituimos $a_{\text {med- } x}$ por $a_x$ en su ecuación:

$$a_x=\frac{v_{2 x}-v_{1 x}}{t_2-t_1}$$

Sean ahora $t_1=0$ y $t_2$ cualquier instante posterior $t$. Simbolizamos con $v_{0 x}$ la componente $x$ de la velocidad en el instante inicial $t=0$; la componente $x$ de la velocidad en el instante posterior $t$ es $v_x$. Entonces, la ecuación se convierte en

$$a_x=\frac{v_x-v_{0 x}}{t-0}$$

o

$$v_x=v_{0 x}+a_x t$$

Podemos interpretar la ecuación como sigue. La aceleración $a_x$ es la tasa constante de cambio de velocidad, es decir, el cambio en la velocidad por unidad de tiempo. El término $a_x t$ es el producto del cambio en la velocidad por unidad de tiempo, $a_x$, y el intervalo de tiempo $t$; por lo tanto, es el cambio total de la velocidad desde el instante inicial $t=0$ hasta un instante posterior $t$. La velocidad $v_x$ en cualquier instante $t$ es entonces la velocidad inicial $v_{0 x}$ (en $t=0$) más el cambio en la velocidad $a_x t$.

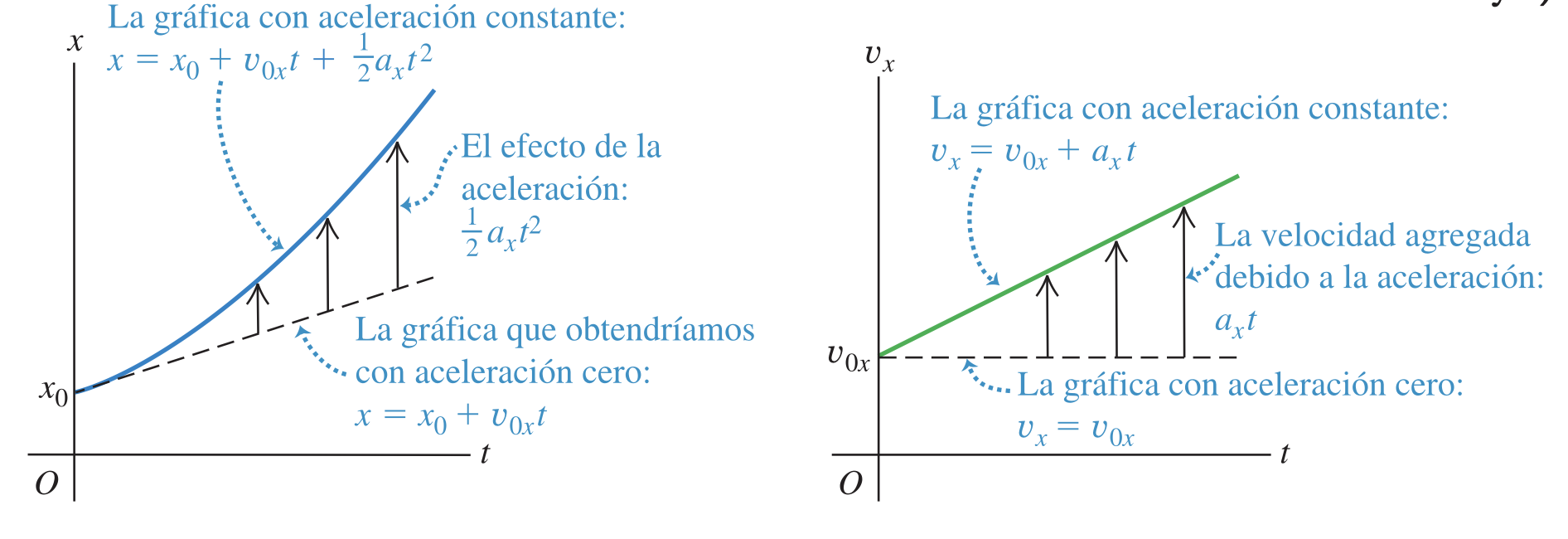
Usando las fórmulas para la velocidad media (bajo el supuesto de aceleración constante), podemos derivar una fórmula para la posición $x$ como función del tiempo. Tenemos que

$$v_{\text {med }-x}=\frac{x-x_0}{t} \qquad v_{\text {med }-x}=\frac{v_{0 x}+v_x}{2}$$

Sustituyendo estas ecuaciones en la ecuación de velocidad, tenemos que

$$x=x_0+v_{0 x} t+\frac{1}{2} a_x t^2$$

Esta ecuación indica que si, en el instante $t=0$, una partícula está en $x_0$ y tiene velocidad $v_{0 x}$, su nueva posición $x$ en un $t$ posterior es la suma de tres términos: su posición inicial $x_0$, más la distancia $v_{0 x} t$ que recorrería si su velocidad fuera constante, y una distancia adicional $\frac{1}{2} a_x t^2$ causada por el cambio de velocidad.

Si queremos relacionar posición, velocidad y aceleración con ecuaciones que no incluyan el tiempo, podemos usar

$$v_x^2=v_{0 x}^2+2 a_x\left(x-x_0\right)$$

Además, una ecuación útil para cuando se desconoce la aceleración es

$$x-x_0=\left(\frac{v_{0 x}+v_x}{2}\right) t$$